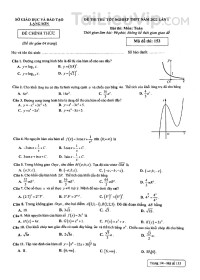
TRƯỜNG THPTCHUYÊN HẠ LONG ĐỀ CHÍNH THỨC Câu 1. Nghiệm của bất phương trình A. . B. . C. . D. . Câu 2. Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?A. . B. . C. . D. . Câu 3. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng A. . B. . C. . D. . Câu 4. Cho hàm số có đạo hàm trên và có bảng biến thiên như sau Giá trị cực đại của hàm số là A. . B. . C. . D. . Câu 5. Cho hàm số có đồ thị như sau.Hàm số trên đồng biến trên khoảng nào dưới đây? A. . B. . C. . D. . Câu 6. Tìm họ nguyên hàm của hàm số . A. . B. . C. . D. . Câu 7. Tiệm cận đứng của đồ thị hàm số là A. . B. . C. . D. . Câu 8. Trong không gian , phương trình mặt cầu có tâm và bán kính là A. . B. . KÌ THI THỬ TN THPT LẦN 1 NĂM HỌC 2021 - 2022MÔN TOÁNThời gian làm bài: 90 phút (không kể thời gian giao đề)( )2log 1 3x− 9x 19x 10x 1 10x 211xyx+=− 3231y x x = − − 4221y x x = − + − 4221y x x = − − 332y x x = − + 1− 2 0 2− ()y f x = f ( x )f' ( x ) x + ∞- ∞ -24 +-+ 00 + ∞3-1- ∞ 2− 4 3 1− ()fx yx-2-1-1O 11 ( )0;1 ( )0;+ ( )2; 1−− ( )1;+ ( )2021f x x = ( )20201d.2020f x x x C=+ ( )20221d.2022f x x x C=+ ( )2000d 2021.f x x x C =+ ( )2022df x x x C =+ 211xyx−=+ 1x = 1x =− 1y =− 2y = Oxyz ( )S ( )1; 0; 3I − 5R = ( ) ( )2221 3 5x y z − + + + = ( ) ( )2221 3 5x y z + + + − =C. . D. . Câu 9. Cho hàm số và cùng liên tục trên . Khẳng định nào đúng? A. . B. . C. . D. Câu 10. Cho hàm số có đạo hàm trên và có bảng xét dấu đạo hàm như sau Hàm số có bao nhiêu điểm cực tiểu? A. 2. B. 3. C. 5. D. 4. Câu 11. Diện tích của mặt cầu có bán kính được tính theo công thức nào sau đây? A. B. C. D. Câu 12. Tìm họ nguyên hàm của hàm số trên khoảng và . A. B. . C. . D. . Câu 13. Có bao nhiêu số tự nhiên có hai chữ số ? A. . B. . C. . D. . Câu 14. Thể tích khối chóp có đôi một vuông góc và là A. . B. . C. . D. . Câu 15. Tìm đạo hàm của hàm số A. . B. . C. . D. . Câu 16. Thể tích khối lập phương cạnh là A. . B. . C. . D. . Câu 17. Nghiệm của phương trình là A. . B. . C. . D. . Câu 18. Cho khối nón có đường cao độ dài đường sinh và bán kính đáy Diện tích xung quanh của khối nón được tính theo công thức nào dưới đây? A. . B. . C. . D. . Câu 19. Tập xác định của hàm số là A. . B. . C. . D. . Câu 20. Trong không gian , cho . Tìm tọa độ véctơ . A. . B. . C. . D. . Câu 21. Cho khối chóp có đáy là tam giác đều cạnh , tam giác vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp theo . A. . B. . C. . D. . ()()2221 3 25x y z+ + + − = ()()2221 3 25x y z− + + + = ()fx ()gx ()()()()d d df x g x x f x x g x x+ = + ()()()()dddf x xfxxgxg x x= ()()d d ,kf x x k f x x k= ()()()()()(). d d . df x g x x f x x g x x= ()fx ()fx S R 21.3SR= 2.SR= 24.3SR= 24.SR= ()1fxx= ();0− ()0;+ ()21d.f x x Cx=+ ()d lnf x x x C=+ ()21df x x Cx−=+ ()d lnf x x x C=+ 210C 81 100 90 V .S ABC , , SA SB SC , 2 , 3SA a SB a SC a= = = 33Va= 32Va= 36Va= 3Va= 2022xy= 1.2022xyx−= 2022ln 2022xy= 2022 .ln 2022xy= 2022x V 3a 381Va= 39Va= 3Va= 327Va= 35x 3log 5x 3log 3x 3log 5x 3log 3x ,h l .r xqS xqS rl= 12xqS rl= 2xqS rl= xqS rh= ()321yx=− ()1;+ \1 ();1− )1;+ Oxyz ()()1; 2; 3 , 3; 5; 2AB−− AB ()2; 7; 5AB= − − ()2; 7;5AB= − − ()2; 7; 5AB= − − ()2; 7;5AB=− .S ABC a SAB S .S ABC a 3324a 338a 336a 3312aCâu 22. Trong không gian , cho hai véc tơ và . Tính góc giữa hai véc tơ đó. A. . B. . C. . D. . Câu 23. Trong một lớp có học sinh nam và học sinh nữ. Chọn ngẫu nhiên học sinh, tính xác suất để học sinh được chọn có cùng giới tính. A. . B. . C. . D. . Câu 24. Tìm họ nguyên hàm của hàm số A. . B. . C. . D. . Câu 25. Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính giá trị A. . B. . C. . D. . Câu 26. Cho hàm số có bảng biến thiên như hình vẽ Hỏi phương trình có bao nhiêu nghiệm? A. . B. . C. . D. . Câu 27. Cho khối nón có bán kính đáy và chiều cao . Thể tích khối nón đã cho bằng A. . B. . C. . D. . Câu 28. Tính tổng các nghiệm của phương trình A. . B. . C. . D. . Câu 29. Với là các số thực dương tùy ý và . Ta có bằng A. . B. . C. . D. . Câu 30. Cho cấp số cộng , biết . Tìm công sai của cấp số cộng A. . B. . C. . D. . Câu 31. Cho khối lăng trụ đứng có tam giác đều cạnh và độ dài cạnh bên . Tính thể tích của khối lăng trụ . A. . B. . C. . D. . Câu 32. Cho hình chóp có đáy là tam giác đều cạnh và . Tính khoảng cách từ đến . A. . B. . C. . D. . Câu 33. Cho khối lăng trụ có thể tích và là trung điểm của cạnh , thể tích khối chóp là A. . B. . C. . D. . Oxyz ()1; 2; 0a= ()1; 3; 0b=− 45 135 30 60 20 15 3 3 90119 29119 80119 39119 ()1xf x e=− ()dxf x x e x C= + + ()dxf x x xe C=+ ()dxf x x e x C= − + ()1dxf x x e C−=+ ,Mm 323y x x=− 2;1− T M m=+ 2 4− 24− 20− ()fx ()25fx= 0 2 1 3 3r= 2h= 6 18 2 4 112 2 5xx+−+= 0 2 12 2− ,ab 1a ()3logaab 3.logab 1. log3ab 1log3ab+ 3 logab+ ()nu 5120uu−= d 4d= 5d= 4d=− 5d=− .ABC A B C ABC a 2a V .ABC A B C 334aV= 323Va= 332aV= 33Va= .S ABC a ()SA ABC⊥ C ()SAB 34a 32a 23a a .ABC A B C V M AA .M ABC 6V 4V 2V 3VCâu 34. Thể tích của khối cầu có bán kính là A. . B. . C. . D. . Câu 35. Cho khối trụ có thiết diện qua trục là hình vuông cạnh . Diện tích xung quanh của khối trụ đã cho bằng A. . B. . C. . D. . Câu 36. Cho bất phương trình . Tập hợp các giá trị của để bất phương trình trên có nghiệm . Giá trị của biểu thức là A. . B. . C. . D. . Câu 37. Cho hàm số xác định và có đạo hàm trên . Hàm số có bảng biến thiên như hình vẽ dưới đây Tính tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . A. . B. . C. . D. . Câu 38. Cho hình trụ tròn xoay có hai đáy là hai hình tròn và . Tồn tại dây cung thuộc đường tròn sao cho là tam giác đều và mặt phẳng hợp với mặt phẳng chứa đường tròn một góc . Khi đó diện tích xung quanh hình trụ là A. . B. . C. . D. . Câu 39. Nguyên hàm của hàm số là A. B. . C. . D. . Câu 40. Cho . Tinh theo và . A. . B. . C. . D. . Câu 41. Cho khối chóp có đáy là hình vuông cạnh , hai mặt phẳng cùng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là . Tính góc giữa đường thẳng và mặt phẳng . A. . B. . C. . D. . Câu 42. Tứ diện có là tam giác đều. Góc giữa hai mặt phẳng và là . Hình cầu tâm bán kính bằng tiếp xúc và mặt phẳng . Gọi là hình chiếu vuông góc của trên mặt phẳng , nằm trong tam giác . Biết rằng thuộc đường thẳng và . Tính thể tích tứ diện . A. . B. . C. . D. . V ()2Rm= ()3163Vm= ()316Vm= ()3323Vm= ()332Vm= 6 72 18 36 12 ()()223 2 2 211log 3 2 1 log 1mmx m x mx m m x+++ − − − + + − m ();ab 22ab+ 3 8 5 9 ()y f x= \2 ()fx ()126yfx=+ 6 5 3 4 ();OR ();OR AB ()O O AB ()O AB ()O 60 xqS 247xqRS= 237xqRS= 2377xqRS= 2677xqRS= ()( ) 2 1 2 sinxxf x x−= + 12cos1xxCx+−++ 2cosln 2xxC−+ 2cosln 2xxC++ 12cos1xxCx−+++ 52log 5 ; log 3ab== 5log 24 a b 53log 24abb+= 53log 24aba+= 53log 24aba+= 5log 243abab+= .S ABCD ABCD a ()(),SAB SAD .S ABCD 33a SB ()SCD 45= 90= 30= 60= ABCD ABC ()BCD ()ABC 60 O 1 ,AB AC ()BCD H D ()ABC H ABC O DH 2ABDH= ABCD 3 324 2 938Câu 43. Trong mặt phẳng tọa độ cho các điểm , , . Gọi là điểm trong không gian thỏa mãn . Tính với . A. . B. . C. . D. . Câu 44. Biết . Tính giá trị biểu thức . A. . B. . C. . D. . Câu 45. Cho hình chóp có đáy ABCD là hình vuông cạnh , vuông góc với đáy, . Khi tam giác quay quanh cạnh thì đường gấp khúc SCA tạo thành hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là A. . B. . C. . D. . Câu 46. Cho . Gọi là tập hợp các giá trị của để bất phương trình có hữu hạn nghiệm nguyên. Tính A. . B. . C. . D. . Câu 47. Cho các số thực thoả mãn .Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính A. . B. . C. . D. . Câu 48. Cho hình chóp có đáy là hình vuông cạnh và vuông góc với đáy. Lấy điểm trên cạnh sao cho . Gọi là hình nón có đỉnh , các điểm thuộc mặt xung quanh, điểm thuộc mặt đáy của hình nón. Tính diện tích xung quanh của . A. . B. . C. . D. . Câu 49. Cho hàm số . Gọi là tập hợp các giá trị của sao cho đồ thị hàm số đã cho có đúng hai điểm cực trị và đường thẳng nối hai điểm cực trị của đồ thị hàm số cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng . Tính tổng các phần tử của A. . B. C. . D. . Câu 50. Trong không gian với hệ tọa độ , cho điểm . Một mặt cầu bất kỳ đi qua và cắt các trục tọa độ lần lượt tại . Biết rằng khi mặt cầu thay đổi nhưng vẫn thỏa đề bài, trọng tâm của tam giác luôn nằm trên một mặt phẳng cố định. Mặt phẳng cố định này chắn các trục tọa độ thành một tứ diện, tính thể tích của khối tứ diện đó. A. . B. . C. . D. . ----HẾT---- Oxy ()2; 0; 2A ()0; 2; 0B ()1; 0; 3C M 2 2 2MA MC MB+= MP ()3; 2; 5P− 2 2 25 26 ()()2020*2022111d . , 1; ,11bxxx C x a baxx−−= + ++ aAb= 2021 2 3 2020 .S ABCD a SA 6SC a= SAC SA 333a 336a 323a 343a 01m ();ab m ()()log 1 8 2 1xmmx−− − ba− 1 3 2 1− 2 2 1− 4 2 1− ,xy 22max 5; 9 7 20 2 81x y x y xy+ − + + ,Mm 2P x y=− Mm− 1 3 5+ 22 1 2 2+ 2 3 5+ .S ABCD ABCD ,7a SA a= M SC CM a ()C C ,,B M D A ()C 216 715a 28 3015a 232 215a 216 39a ()22251+ + +=+mx m xyx S m 254 S 0 1 4− 2− Oxyz ()2; 3; 4N O N ,,Ox Oy Oz , , 0A B C G ABC 243893888 243894374 243898748 243892916ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 A D B B D B B D A A D D D D C D C A A D A A B C D 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 D A A D B C B A C C D D D B C C D D B D A A B C A Câu 1. Nghiệm của bất phương trình A. . B. . C. . D. . Lời giải Chọn A Điều kiện: . Vậy tập nghiệm của bất phương trình là . Câu 2. Đường cong hình bên là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào? A. . B. . C. . D. . Lời giải Chọn D Đồ thị đã cho là đồ thị của hàm số bậc có hệ số và có điểm cực trị. Câu 3. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng A. . B. . C. . D. . Lời giải Chọn B Giao điểm của đồ thị hàm số với trục tung có . Câu 4. Cho hàm số có đạo hàm trên và có bảng biến thiên như sau Giá trị cực đại của hàm số là A. . B. . C. . D. . Lời giải Chọn B Giá trị cực đại của hàm số là . Câu 5. Cho hàm số có đồ thị như sau. ( )2log 1 3x− 9x 19x 10x 1 10x 1x ()2log 1 3 1 8 9x x x− − 9x 211xyx+=− 3231y x x = − − 4221y x x = − + − 4221y x x = − − 4 42y ax bx c= + + 0a 3 332y x x = − + 1− 2 0 2− 332y x x = − + 02xy= = ()y f x = f ( x )f' ( x ) x + ∞- ∞ -24 +-+ 00 + ∞3-1- ∞ 2− 4 3 1− 4 ()fxHàm số trên đồng biến trên khoảng nào dưới đây? A. . B. . C. . D. . Lời giải Chọn D Hàm số đồng biến trên khoảng . Câu 6. Tìm họ nguyên hàm của hàm số . A. . B. . C. . D. . Lời giải Chọn B Câu 7. Tiệm cận đứng của đồ thị hàm số là A. . B. . C. . D. . Lời giải Chọn B Ta có và . Nên đồ thị hàm số đã cho có tiệm cận đứng . Câu 8. Trong không gian , phương trình mặt cầu có tâm và bán kính là A. . B. . C. . D. . Lời giải Chọn D Phương trình mặt cầu có tâm và bán kính là . Câu 9. Cho hàm số và cùng liên tục trên . Khẳng định nào đúng? A. . B. . C. . D. Lời giải Chọn A Nhận định đúng là . Câu 10. Cho hàm số có đạo hàm trên và có bảng xét dấu đạo hàm như sau Hàm số có bao nhiêu điểm cực tiểu? yx-2-1-1O 11 ( )0;1 ( )0;+ ( )2; 1−− ( )1;+ ()1;+ ( )2021f x x = ( )20201d.2020f x x x C=+ ( )20221d.2022f x x x C=+ ( )2000d 2021.f x x x C =+ ( )2022df x x x C =+ 211xyx−=+ 1x = 1x =− 1y =− 2y = ()()1121lim lim1xxxyx++→ − → −−= = ++ ()()1121lim lim1xxxyx−−→ − → −−= = −+ 1x=− Oxyz ( )S ( )1; 0; 3I − 5R = ( ) ( )2221 3 5x y z − + + + = ( ) ( )2221 3 5x y z + + + − = ()()2221 3 25x y z+ + + − = ()()2221 3 25x y z− + + + = ()1; 0; 3I− 5R= ()()()222: 1 3 25S x y z− + + + = ()fx ()gx ()()()()d d df x g x x f x x g x x+ = + ()()()()dddf x xfxxgxg x x= ()()d d ,kf x x k f x x k= ()()()()()(). d d . df x g x x f x x g x x= ()()()()d d df x g x x f x x g x x+ = + ()fx ()fxA. 2. B. 3. C. 5. D. 4. Lời giải Chọn A Dựa vào bảng xét dấu đạo hàm, ta thấy hàm số có 2 điểm cực tiểu. Câu 11. Diện tích của mặt cầu có bán kính được tính theo công thức nào sau đây? A. B. C. D. Lời giải Chọn D Công thức tính diện tích mặt cầu là Câu 12. Tìm họ nguyên hàm của hàm số trên khoảng và . A. B. . C. . D. . Lời giải Chọn D . Câu 13. Có bao nhiêu số tự nhiên có hai chữ số ? A. . B. . C. . D. . Lời giải Chọn D Số tự nhiên có hai chữ số có (số). Câu 14. Thể tích khối chóp có đôi một vuông góc và là A.. B. . C. . D.. Lời giải Chọn D Ta có . Câu 15. Tìm đạo hàm của hàm số A. . B.. C.. D.. Lời giải Chọn C Câu 16. Thể tích khối lập phương cạnh là A. . B. . C. . D. . Lời giải Chọn D Thể tích khối lập phương cạnh là . Câu 17. Nghiệm của phương trình là A. . B. . C. . D. . Lời giải Chọn C Ta có . Câu 18. Cho khối nón có đường cao độ dài đường sinh và bán kính đáy Diện tích xung quanh của khối nón được tính theo công thức nào dưới đây? A. . B. . C. . D. . Lời giải S R 21.3SR= 2.SR= 24.3SR= 24.SR= 24.SR= ()1fxx= ();0− ()0;+ ()21d.f x x Cx=+ ()d lnf x x x C=+ ()21df x x Cx−=+ ()d lnf x x x C=+ ()d lnf x x x C=+ 210C 81 100 90 9.10 90= V .S ABC , , SA SB SC , 2 , 3SA a SB a SC a= = = 33Va= 32Va= 36Va= 3Va= 311. . .2 .366V SA SB SC a a a a= = = 2022xy= 1.2022xyx−= 2022ln 2022xy= 2022 .ln 2022xy= 2022x V 3a 381Va= 39Va= 3Va= 327Va= V 3a ()333 27V a a== 35x 3log 5x 3log 3x 3log 5x 3log 3x 33 5 log 5xx ,h l .r xqS xqS rl= 12xqS rl= 2xqS rl= xqS rh=Chọn A Câu 19. Tập xác định của hàm số là A. . B. . C. . D. . Lời giải Chọn A ĐK: . Vậy tập xác định của hàm số là Câu 20. Trong không gian , cho . Tìm tọa độ véctơ . A. . B. . C. . D. . Lời giải Chọn D . Câu 21. Cho khối chóp có đáy là tam giác đều cạnh , tam giác vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp theo . A. . B. . C. . D. . Lời giải Chọn A Vì tam giác cân tại nên hạ là trung điểm . Vì Tam giác vuông cân tại nên Câu 22. Trong không gian , cho hai véc tơ và . Tính góc giữa hai véc tơ đó. A. . B. . C. . D. . Lời giải Chọn A Ta có . ()321yx=− ()1;+ \1 ();1− )1;+ 1 0 1xx− ()1;D= + Oxyz ()()1; 2; 3 , 3; 5; 2AB−− AB ()2; 7; 5AB= − − ()2; 7;5AB= − − ()2; 7; 5AB= − − ()2; 7;5AB=− ()()()()3 1; 5 2; 2 3 2; 7; 5AB= − − − − − = − .S ABC a SAB S .S ABC a 3324a 338a 336a 3312a SAB S SH AB⊥ H AB ()()()()()SAB ABCSAB ABC AB SH ABCSH AB⊥ = ⊥⊥ SAB S 2aSA SB== 22AB aSH== 22.1 1 3 3. . .3 3 2 4 24S ABC ABCa a aV SH S= = = Oxyz ()1; 2; 0a= ()1; 3; 0b=− 45 135 30 60 ()().1cos , , 452.aba b a bab= = = Câu 23. Trong một lớp có học sinh nam và học sinh nữ. Chọn ngẫu nhiên học sinh, tính xác suất để học sinh được chọn có cùng giới tính. A. . B. . C. . D. . Lời giải Chọn B Ta có số phần tử của không gian mẫu là: cách chọn Số phần tử của biến cố “Ba học sinh được chọn có cùng giới tính” là: Xác suất của biến cố là: . Câu 24. Tìm họ nguyên hàm của hàm số A. . B. . C. . D. . Lời giải Chọn C Ta có họ nguyên hàm của hàm số là: . Câu 25. Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính giá trị A. . B. . C. . D.. Lời giải Chọn D Ta có: . . tại . tại . Vậy . Câu 26. Cho hàm số có bảng biến thiên như hình vẽ Hỏi phương trình có bao nhiêu nghiệm? A. . B. . C. . D. . Lời giải Chọn D Ta có: . Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số và 20 15 3 3 90119 29119 80119 39119 ()335nC= A ()3320 15n A C C=+ A ()29119PA= ()1xf x e=− ()dxf x x e x C= + + ()dxf x x xe C=+ ()dxf x x e x C= − + ()1dxf x x e C−=+ ()1xf x e=− ()dxf x x e x C= − + ,Mm 323y x x=− 2;1− T M m=+ 2 4− 24− 20− 236y x x=− 20 2;10 3 6 02 2;1xy x xx= −= − = −= ()()()2 20; 0 0; 1 2y y y− = − = = − 2;1max 0My−== 0x= 2;1min 20my−= = − 2x=− 20T M m= + = ()fx ()25fx= 0 2 1 3 ()()5252f x f x= = () y f x=đường thẳng . Từ đồ thị ta thấy có ba giao điểm. Vậy phương trình có ba nghiệm. Câu 27. Cho khối nón có bán kính đáy và chiều cao . Thể tích khối nón đã cho bằng A. . B. . C. . D. . Lời giải Chọn A Thể tích khối nón là: Câu 28. Tính tổng các nghiệm của phương trình A. . B. . C. . D. . Lời giải Chọn A Ta có: . Đặt , phương trình trở thành: . Vậy tổng tất cả các nghiệm của phương trình là 0. Câu 29. Với là các số thực dương tùy ý và . Ta có bằng A. . B. . C. . D. . Lời giải Chọn D Ta có: . Câu 30. Cho cấp số cộng , biết . Tìm công sai của cấp số cộng A. . B. . C. . D. . Lời giải Chọn B Ta có: . Câu 31. Cho khối lăng trụ đứng có tam giác đều cạnh và độ dài cạnh bên . Tính thể tích của khối lăng trụ . A. . B. . C. . D. . Lời giải Chọn C Thể tích khối lăng trụ là . 52y= 3r= 2h= 6 18 2 4 2211.3 .2 6 .33V r h = = = 112 2 5xx+−+= 0 2 12 2− 1112 2 5 2.2 2. 52x x xx+−+ = + = ()20xtt= 2222122 5 2 5 2 0111222xxtxt t txtt===+ = − + = =−== ,ab 1a ()3logaab 3.logab 1. log3ab 1log3ab+ 3 logab+ ()()33log log log 3 log , 0; 1a a a aa b a b b a b a= + = + + ()nu 5120uu−= d 4d= 5d= 4d=− 5d=− 5 1 5 1 1 14 20 4 20 4 20 5u u d u u u d u d d= + − = + − = = = .ABC A B C ABC a 2a V .ABC A B C 334aV= 323Va= 332aV= 33Va= 2333. .242ABCaaV S AA a= = =Câu 32. Cho hình chóp có đáy là tam giác đều cạnh và . Tính khoảng cách từ đến . A. . B. . C. . D. . Lời giải Chọn B Gọi là trung điểm của cạnh , ta có nên . Câu 33. Cho khối lăng trụ có thể tích và là trung điểm của cạnh , thể tích khối chóp là A. . B. . C. . D. . Lời giải Chọn A Vì là trung điểm cạnh nên . Mặt khác, vậy nên . Câu 34. Thể tích của khối cầu có bán kính là A. . B. . C. . D. . Lời giải Chọn C Thể tích của khối cầu cần tìm là . .S ABC a ()SA ABC⊥ C ()SAB 34a 32a 23a a H AB ()CH ABCH SABCH SA⊥⊥⊥ ()()3,2ad C SAB CH== .ABC A B C V M AA .M ABC 6V 4V 2V 3V M AA ..12M ABC A ABCVV= ..1133A ABC ABC A B CV V V == ..126M ABC A ABCVVV== V ()2Rm= ()3163Vm= ()316Vm= ()3323Vm= ()332Vm= V 34 3233VR==Câu 35. Cho khối trụ có thiết diện qua trục là hình vuông cạnh . Diện tích xung quanh của khối trụ đã cho bằng A. . B. . C. . D. . Lời giải Chọn C Thiết diện qua trục là hình vuông cạnh nên khối trụ có bán kính , chiều cao . Suy ra diện tích xung quanh của khối trụ là . Câu 36. Cho bất phương trình . Tập hợp các giá trị của để bất phương trình trên có nghiệm . Giá trị của biểu thức là A. . B. . C. . D. . Lời giải Chọn D Ta có Câu 37. Cho hàm số xác định và có đạo hàm trên . Hàm số có bảng biến thiên như hình vẽ dưới đây Tính tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . A. . B. . C. . D. . Lời giải Chọn D Đặt , ta có hàm số xác định trên , trong đó và . Khi đó ta có 6 72 18 36 12 6 3r= 6h= 2 36rh= ()()223 2 2 211log 3 2 1 log 1mmx m x mx m m x+++ − − − + + − m ();ab 22ab+ 3 8 5 9 ()()()()()()()()()()()()()223 2 2 2113 2 2 223 2 22221;11;1log 3 2 1 log 13 2 1 1102 2 01;1201;121;1min max 21;10; 3mmx m x mx m m xx m x mx m m xxx m x mx m mxx m x mxx m xxx m xxm++−−+ − − − + + −+ − − − + + −−+ − − − + −− + − − −− − − 22093aabb= + == ()y f x= \2 ()fx ()126yfx=+ 6 5 3 4 ()()126gxfx=+ \ 2;a ()3fa=− ()2;a +và nên và là hai đường tiệm cận ngang. Mặt khác ta có là tiệm cận đứng; không là tiệm cận đứng; là tiệm cận đứng; Vậy đồ thị hàm số có đường tiệm cận. Câu 38. Cho hình trụ tròn xoay có hai đáy là hai hình tròn và . Tồn tại dây cung thuộc đường tròn sao cho là tam giác đều và mặt phẳng hợp với mặt phẳng chứa đường tròn một góc . Khi đó diện tích xung quanh hình trụ là A. . B. . C. . D. . Lời giải Chọn D Gọi là trung điểm . Khi đó . Xét tam giác vuông tại có và . Mặt khác xét tam giác vuông tại có . Vì tam giác đều nên . Diện tích xung quanh hình trụ . Câu 39. Nguyên hàm của hàm số là A. B. . C. . D. . Lời giải Chọn B ()()1lim 02 lim 6xxgxfx→−→−==+ ()()11lim2 lim 6 26xxgxfx→+→+==+ 0y= 126y= ()()()()221lim 22 lim 6xxg x xfx−−→−→−= = + = −+ ()()221lim 0 22 lim 6xxg x xfx→→= = =+ ()()1lim2 lim 6xaxag x x afx++→→= = + =+ ()126yfx=+ 4 ();OR ();OR AB ()O O AB ()O AB ()O 60 xqS 247xqRS= 237xqRS= 2377xqRS= 2677xqRS= I AB OI AB⊥ O OI O tan 603O O O OOI== 2sin 603O O O OOI== OIA I 222 2 2 2 2 2433OO O OAI R OI R AB R= − = − = − O AB 2 2 2 2 23 3 4 332 4 37RO I AB O I AB O O R O O O O = = = − = 2672.7xqRS R O O== ()( ) 2 1 2 sinxxf x x−= + 12cos1xxCx+−++ 2cosln 2xxC−+ 2cosln 2xxC++ 12cos1xxCx−+++Câu 40. Cho . Tinh theo và . A. . B. . C. . D. . Lời giải Chọn C Câu 41. Cho khối chóp có đáy là hình vuông cạnh , hai mặt phẳng cùng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là . Tính góc giữa đường thẳng và mặt phẳng . A. . B. . C. . D. . Lời giải Chọn C Vì cùng vuông góc với mặt phẳng mà . Suy ra . Ta có . Gọi là hình chiếu vuông góc của lên mặt phẳng . Có . là hình chiếu của lên mặt phẳng . Ta có: . . Vậy góc giữa đường thẳng và mặt phẳng bằng . Câu 42. Tứ diện có là tam giác đều. Góc giữa hai mặt phẳng và là . Hình cầu tâm bán kính bằng tiếp xúc và mặt phẳng . Gọi là hình ()()()2d 2 1 2 sin d 2 sin d cosln 2xx x xf x x x x x x x C−= + = + = − + 52log 5 ; log 3ab== 5log 24 a b 53log 24abb+= 53log 24aba+= 53log 24aba+= 5log 243abab+= 5 5 55log 24 log 8.3 log 8 log 3= = + 5 5 523 3 33.log 2 log 3 log 3log 5abbaa+= + = + = + = .S ABCD ABCD a ()(),SAB SAD .S ABCD 33a SB ()SCD 45= 90= 30= 60= ()(),SAB SAD ()ABCD ()()SAB SAD SA= ()SA ABCD⊥ 322.11..3 3 3S ABCDaV AB SA a SA SA a= = = = H B ()SCD ()SB SCD S= SH SB ()SCD ()()(),,SB SCD SB SH BSH = = = ()()()(),,1sin222d B SCD d A SCDBH SA AD a aSB SB SB SD SBaa= = = = = = 30 = SB ()SCD 30= ABCD ABC ()BCD ()ABC 60 O 1 ,AB AC ()BCD Hchiếu vuông góc của trên mặt phẳng , nằm trong tam giác . Biết rằng thuộc đường thẳng và . Tính thể tích tứ diện . A. . B. . C. . D. . Lời giải Chọn D Gọi là trung điểm của . Kẻ vuông góc với tại ; vuông góc với tại cách đều . Đặt: Lại có: là trọng tâm . Ta có: là trung điểm của là tiếp điểm của mặt cầu với . Lại có: . Câu 43. Trong mặt phẳng tọa độ cho các điểm , , . Gọi là điểm trong không gian thỏa mãn . Tính với . A. . B. . C. . D. . Lời giải D ()ABC H ABC O DH 2ABDH= ABCD 3 324 2 938 N BC OM AB M OP AC P 1OM OP = = HM HP H = ,AB AC H AN ()()()0, 60ABC DBC DNH = = 0226tan 60 3232DH xHNxAB x DHxDN DH HN=== = = + = 3123xAN HN AN N= = ABC ()AB OHM AB HM⊥ ⊥ M AB HM HN OM ON = = 1ON = N ()BCD 2 2 2136 36OH ON NH x = − = − 2136 326xOD OH DH x = + = + − 2 2 21933OD ON ND x= + = + 221136 3 9 3 32 6 3xx x x + − = + = 31 9 32.38934ABCD ABCABCDHV DH SS= = == Oxy ()2; 0; 2A ()0; 2; 0B ()1; 0; 3C M 2 2 2MA MC MB+= MP ()3; 2; 5P− 2 2 25 26Chọn D Gọi là điểm thỏa mãn . Ta có ; ;. Khi đó . Suy ra ; ;. Ta có . Khi đó hay . Câu 44. Biết . Tính giá trị biểu thức . A. . B. . C. . D. . Lời giải Chọn B Ta có Suy ra . Vậy . Câu 45. Cho hình chóp có đáy ABCD là hình vuông cạnh , vuông góc với đáy, . Khi tam giác quay quanh cạnh thì đường gấp khúc SCA tạo thành hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là A. . B. . C. . D. . Lời giải Chọn D Bán kính đáy: . Đường cao của hình nón là . Vậy thể tích khối nón: . ();;I x y z ()*IA IC IB+= ()2 ; ; 2IA x y z= − − − (); 2 ;IB x y z= − − − ()1 ; ; 3IC x y z= − − − ()()2 1 3* 2 2 3; 2; 52 3 5x x x xy y y y I Pz z z z− + − = − = − − = − = − − − + − = − = ()21; 2; 3 14IA IA= − − = ()23; 4; 5 50IB IB= − − = ()22; 2; 2 12IC IC= − − = 2 2 2 2 2 20MA MC MB MA MC MB+ = + − = ()()()2 2 22 2 2MA MC MB MI IA MI IC MI IB+ − = + + + − + 2 2 2 2 2 22 . 2 . 2 .MI IA MI IA MI IC MI IC MI IB MI IB= + + + + + − − − ()()2 2 2 220MI IA IC IB MI IA IC IB= + + − + + − = ()2214 12 50 0 24 2 6MP MP MP + + − = = = ()()2020*2022111d . , 1; ,11bxxx C x a baxx−−= + ++ aAb= 2021 2 3 2020 ()()()20202 2020 20212022 211 1 1 1 1 1 1d . d d .1 2 1 1 4022 111xx x x xx x Cx x x xxx−− − − − = = = + + + + + ++ 40222021ab== 2aAb== .S ABCD a SA 6SC a= SAC SA 333a 336a 323a 343a 2r AC a== SA 222h SA SC AC a = = − = 321433aV r h==Câu 46. Cho . Gọi là tập hợp các giá trị của để bất phương trình có hữu hạn nghiệm nguyên. Tính A. . B.. C. . D. . Lời giải Chọn A Trường hợp 1: Ta có: . Rỏ ràng trong trường hợp này không thể có hữu hạn nghiệm nguyên Trường hợp 2: Ta có: Để bất phương trình có hữu hạn nghiệm nguyên thì: Vậy Câu 47. Cho các số thực thoả mãn .Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính A. . B. . C. . D. . Lời giải Chọn A Từ giả thiết ta có . 01m ();ab m ()()log 1 8 2 1xmmx−− − ba− 1 3 2 1− 2 2 1− 4 2 1− 1m ()()2 2 2 2log 1 8 2 1 1 8 . 8 1 0x x x x xmm x m m m m m− − − − −− − − + − 2 2 22 2 216 4 16 4 16 40 log logxmmm m mm x xm m m− + − + − + − − − 01m ()()2222. 8 1 018log 1 8 2 111 8 08xxxxxmxxm m mmmmxmm−−−−−−−+ − −− − − 22222216 416 4 16 4log log1log 8 log 8log8xmmmmmmmmmxxmmmxxx−+−+ − + − − − − 2 2 22 2 216 4 8 16 32 8 16 32log 8 log 0 log 0 1m m mm m mm m m+ − + − + −+ ()2 2 48 16 32 0, 0;1m m m m + + 1ba−= ,xy 22max 5; 9 7 20 2 81x y x y xy+ − + + ,Mm 2P x y=− Mm− 1 3 5+ 22 1 2 2+ 2 3 5+ ()2222225199 7 252 2 2xyxyxy+− + − + − Tập hợp điểm thoả mãn yêu cầu bài là phần được tô trên hình vẽ kể cả biên. Ta thấy cắt tại hai điểm phân biệt trong đó có điểm thoả mãn yêu cầu bài toán. Xét đường thẳng đi qua thoả mãn yêu cầu bài toán: . đạt GTNN khi đi qua nên . . +. . cắt tại điểm thoả mãn bài toán. Khi đó . Vậy . Câu 48. Cho hình chóp có đáy là hình vuông cạnh và vuông góc với đáy. Lấy điểm trên cạnh sao cho . Gọi là hình nón có đỉnh , các điểm thuộc mặt xung quanh, điểm thuộc mặt đáy của hình nón. Tính diện tích xung quanh của . A. . B. . C. . D. . Lời giải Chọn B Lấy điểm thuộc đoạn thẳng sao cho . Gọi hình nón ngoại tiếp hình chóp có đỉnh . Gọi . nên thuộc mặt đáy của hình nón và , điểm thuộc mặt đáy của hình nón . Hơn nữa suy ra vuông góc với trục của hình nón và thiết diện của với mặt xung quanh của hình nón là đường tròn, đồng thời song song với mặt chứa đáy của hình nón . Từ và suy ra hình nón đồng dạng với hình nón với tỷ số . . (),xy ()1C ()3C ()2,1 (),xy 2x y c−= 2xy− ()2,1 0m= ()()22 2 22: 2 8 1 9C x y x x y+ = + − + = ()()()()22 1 2 1 1 2 .9 1 3 5 1x y x y− = − + − + + − + = + 1: 2 1 3 5 0xy − − − = 1 ()2C 3 5 1M=+ 3 5 1Mm− = + .S ABCD ABCD ,7a SA a= M SC CM a ()C C ,,B M D A ()C 216 715a 28 3015a 232 215a 216 39a E SC CE a= ()1C .C BDE C O AC BD= O BD ()1C 2CA CO= A ()C ()1 CB CD CE a= = = ()BDE ()C ()BDE ()C ()BDE ()C ()2 ()1 ()2 ()1C ()C 12 2 2 2 21 2 2 3 4 1 303 , cos , 2 ,3 3 3 3 2 6SC a SCB ED EB a a a EO a a a= = = = − = = − = 21 30 15. 2.2 6 6EBDaS a a==. Diện tích xung quanh của hình nón : Câu 49. Cho hàm số . Gọi là tập hợp các giá trị của sao cho đồ thị hàm số đã cho có đúng hai điểm cực trị và đường thẳng nối hai điểm cực trị của đồ thị hàm số cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng . Tính tổng các phần tử của A. . B. C.. D. . Lời giải Chọn C Ta có: . Với ta có có hai nghiệm phân biệt thỏa . Mặt khác, đường thẳng qua hai điểm cực trị của đồ thị hàm số là . Gọi và . Do đó: . Do đó . Câu 50. Trong không gian với hệ tọa độ , cho điểm . Một mặt cầu bất kỳ đi qua và cắt các trục tọa độ lần lượt tại . Biết rằng khi mặt cầu thay đổi nhưng vẫn thỏa đề bài, trọng tâm của tam giác luôn nằm trên một mặt phẳng cố định. Mặt phẳng cố định này chắn các trục tọa độ thành một tứ diện, tính thể tích của khối tứ diện đó. A. . B. . C. . D. . Lời giải Chọn A Giả sử , và . Khi đó là tâm của mặt cầu có tọa độ là . Theo tính chất hình hộp, ta có . Do thuộc mặt phẳng trung trực của đoạn Suy ra . 224.22 30315154.6BDEaaRaa== ()C 24 30 8 30. .2 .15 15xqaS a a== ()22251+ + +=+mx m xyx S m 254 S 0 1 4− 2− ()2251m x mymx+ + −= + + ()()()2222 2 5 2'1m x m x myx− + + − + +=+ 2m − '0y= 12,xx ()12121252xxmxxm=−−+=+ ()2 2 4.5.12:54.1 2mxmyx− + −+ = = +− 10;02A Ox Am= −+ ()0; 5B Oy B= 225 1 25 5 10 25. . . 2 464 2 4 2 2 4OABmS OB OA mmm== = = + = =−+ 124mm+ = − Oxyz ()2; 3; 4N O N ,,Ox Oy Oz , , 0A B C G ABC 243893888 243894374 243898748 243892916 ()(); 0; 0A a S Ox= ()()0; ; 0B b S Oy= ()()0; 0;C c S Oz= I ;;2 2 2a b cI 2;;3 3 3 3abcOG OI G= (),O N S IO IN= I ON 2 3 4 29a b c + + = 29 292. 3. 4. 2 3 43 3 3 3 3G G Ga b cx y z+ + = + + = ()29: 2 3 43G P x y z + + =Gọi , Và . Vậy . _______________ TOANMATH.com _______________ ()29; 0; 06M P Ox M= ()290; ; 09N P Oy N= ()290; 0;12P P Oz P= 1 24389..6 3888OMNPV OM ON OP==
- Xem thêm -