Bộ đề thi tham khảo học kỳ 2 môn Toán 12 mới nhất (có đáp án và giải chi tiết)
2,030 5

Tải về máy để xem đầy đủ hơn, bản xem trước là bản PDF
Tags: #toán 12#đề thi toán 12#thptqg toán
Mô tả chi tiết
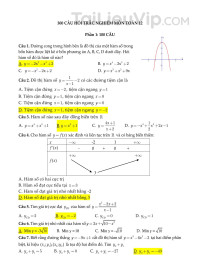
Bộ đề thi tham khảo học kỳ 2 môn Toán 12 mới nhất (có đáp án và giải chi tiết) ược soạn dưới dạng file word và PDF gồm 48 trang.

Nội dung
www.thuvienhoclieu .comwww.thuvienhoclieu.comĐ 1Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ng ặ ẳ: 2 3 0P x z . Vect nào d iơ ướđây là m t vect pháp tuy n c a ộ ơ ế ủP ?A. 11; 2; 3n . B. 21; 2; 0n . C. 30;1; 2n . D.41; 0; 2n .Câu 2. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t c u ặ ầ2 2 2: 2 4 6 0.S x y z x y z Đ ng tròn giao tuy n c aườ ế ủ m t c uặ ầ S v i m t ph ng ớ ặ ẳOxy có bán kính làA. 3r . B. 5r . C. 6r . D. 14r .Câu 3. Tìm nguyên hàm c a hàm s ủ ố34 2f x x x . A.2 2( )d 12f x x x x C . B.4 24( )d3f x x x x C .C.2( )d 12 2f x x x C . D.4 2( )df x x x x C . Câu 4. Ph ng trình nào d i đây nh n hai s ph c ươ ướ ậ ố ứ1 3i và 1 3i làm nghi mệA.22 4 0z z . B.22 4 0z z . C.22 4 0z z . D.22 4 0z z . Câu 5. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai vect ơ1; 2 ; 0a và 2 ; 0 ;1b . cos ,a b b ngằA.2cos ,5a b . B.2cos ,25a b . C.2cos ,5a b . D.2cos ,25a b . Câu 6. Cho hàm s ốy = f(x) liên t c trên ụ[ ; ]a b . Di n tích ệS c a hình ph ng gi i h n b i đ th c aủ ẳ ớ ạ ở ồ ị ủhàm s ốy = f(x) , tr c hoành và hai đ ng th ng ụ ườ ẳ, x a x b đ c tính theo công th cượ ứA.( )dbaS f x x . B.( ) dbaS f x x . C.2( )dbaS f x x . D.( )dbaS f x x . Câu 7. Tìm t t c các nghi m c a ph ng trình ấ ả ệ ủ ươ22 5 0z z trên t p s ph c ậ ố ứ .A . 1 2 ,1 2i i . B.1 ,1i i C.1 2 , 1 2i i D.1 , 1i i Câu 8. Tìm h nguyên hàm c a hàm s ọ ủ ố5 3( )xf x e .A. 5 31( ) d3xf x x e C . B. 5 3( ) dxf x x e C .C. 5 31( ) d5xf x x e C . D. 5 3( ) d 5xf x x e C .Câu 9. Trong không gian Oxyz , cho m t ph ng ặ ẳ: 3 4 2 4 0P x y z và đi m ể1; 2; 3A .Kho ng cách t ả ừA đ n ếP b ngằA. 59 . B. 529 . C. 529 . D. 53 . www.thuvienhoclieu .com Trang 1www.thuvienhoclieu .comCâu 10. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , to đ giao đi m ạ ộ ểM c a đ ng th ngủ ườ ẳ12 9 1:4 3 1x y zd và m t ph ng ặ ẳ: 3 5 2 0P x y z là A.1; 0; 1 . B.0; 0; 2 . C.1;1; 6 . D.12; 9;1 . Câu 11. Trong không gian Oxyz , đ dài c a vect ộ ủ ơ3; 4; 0u b ngằA. 1. B. 5. C. 25. D. 5.Câu 12. Cho hình ph ng ẳ D gi i h n b i đ ng cong ớ ạ ở ườ212y x x , tr c hoành và các đ ng th ng ụ ườ ẳ1,x4x. Kh i tròn xoay t o thành khi quay hình ố ạ D quanh tr c hoành có th tích b ngụ ể ằA. 425 . B. 3 . C. 12825 . D. 415 .Câu 13. Ph n o c a s ph cầ ả ủ ố ứ2 3z i làA.3 . B. 3i . C.3 . D.3i . Câu 14. Gi s hàm s ả ử ốy f x liên t c nh n giá tr d ng trên ụ ậ ị ươ0; và th a mãn ỏ1 1f ,. 3 1f x f x x , v i m i ớ ọ0x . M nh đ nào sau đây đúng?ệ ềA. 3 5 4f . B. 1 5 2f .C. 4 5 5f . D. 2 5 3f .Câu 15. Cho các hàm s ốf x , g x liên t c trên t p xác đ nh. M nh đ nào sau đây ụ ậ ị ệ ề sai ?A.d d df x g x x f x x g x x . B.dddf x xf xxg xg x x .C.df x x f x C . D.. d dk f x x k f x x , 0k . Câu 16. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , m t c u nào d i đây có tâm thu c đ ng th ng ặ ầ ướ ộ ườ ẳOz?A.2 2 26 10 0x y z y B. 2 2 22 6 8 0x y z x z C.2 2 26 10 0x y z x D. 2 2 22 8 0x y z z Câu 17. Trong không gian v i h t a đ ớ ệ ọ ộOxyz, cho m t c uặ ầ Scó ph ng trình làươ:2 2 22 4 6 9 0x y z x y z . M t c uặ ầ Scó tâm I bán kínhR làA. 1; 2 ; 3I và 5R . B. 1; 2 ; 3I và 5R .C. 1; 2 ; 3I và 5R . D. 1; 2 ; 3I và 5R .Câu 18. Tính 102 5 dI x x .A. 2 . B. 4 . C. 4 . D. 3 . www.thuvienhoclieu .com Trang 2www.thuvienhoclieu .comCâu 19. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , m t c u có tâm ặ ầ1; 2; 3A và bán kính 6R cóph ng trình ươA.2 2 21 2 3 36x y z . B.2 2 21 2 3 36x y z .C.2 2 21 2 3 36x y z . D.2 2 21 2 3 6x y z . Câu 20. Th tích kh i tròn xoay t o thành khi quay hình ph ng gi i h n b i các đ ng ể ố ạ ẳ ớ ạ ở ườexy x ,0y, 0x , 1x xung quanh tr c ụOx làA. 12 20e dxV x x . B. 120e dxV x x . C. 12 20e dxV x x . D. 10e dxV x x .Câu 21. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , c ho đ ng th ng ườ ẳ1 2: 3 4x td y t tz t . Khi đóph ng trình chính t c c a ươ ắ ủd làA. 2 1 11 3 4x y z . B. 1 3 42 1 1x y z .C.1 3 42 1 1x y z . D. 2 3 52 1 1x y z .Câu 22. Tính 6201dcos 2I xx .A.3I . B.32I . C.32I . D.2 3I . Câu 23. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể; ;H a b c là hình chi u vuông góc c aế ủđi m ể1; 2; 0M lên đ ng th ng ườ ẳ2 1 1:2 1 1x y z . Tính a b .A. 23a b . B. 0a b . C. 1a b . D. 3a b .Câu 24. Cho 22d 1f x x , 42d 4f x x . Tính 42I df x x .A.I 5 . B.I 5 . C.I 3 . D.I 3 .Câu 25. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho ba đi m ể1; 2;1 , 2;1; 3 , 0; 3; 2A B C . Tìm t a đọ ộtr ng tâm ọG c a tam giác ủABC .A. 3; 6; 6G . B. 2 1 2; ;3 3 3G . C. 1 2 2; ;3 3 3G . D. 1; 2; 2G .Câu 26. Cho hàm s ốf x có đ o hàm trên ạ , 1 2f và 3 2f . Tí ch phân 31'I f x dxb ngằA. 4.I B. 3.I C. 0.I D. 4.I www.thuvienhoclieu .com Trang 3www.thuvienhoclieu .comCâu 27. Trong không gian v i h t a đ ớ ệ ọ ộ cho ba đi mể và Véct nào d i đây là véct pháp tuy n c a m t ph ngơ ướ ơ ế ủ ặ ẳ ?A. B. C. D. Câu 28. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai vect ơ1; 2 ; 0a và 2 ; 3;1b . Kh ngẳđ nh nào sau đây là ị SaiA. 1;1; 1a b . B. 14b .C. 2 2 ; 4 ; 0a . D. . 8a b .Câu 29. Cho 92d 6f x x . Tính 22 311 dI x f x x .A. 8.I B. 2.I C. 4I . D. 3.ICâu 30. Di n tích ệS c a hình ph ng gi i h n b i các đ ng ủ ẳ ớ ạ ở ườ21y x , 2y , 0x và 1x đ cượtính b i công th c nào d i đây?ở ứ ướA. 120( 1)dS x x . B. 120( 1)dS x x .C. 120( 3)dS x x . D. 120( 3)dS x x .Câu 31. Cho hai s ph c ố ứ12 4z i và 21 3 .z i Ph n o c a s ph c ầ ả ủ ố ứ1 2z i z b ngằA. 1 . B. 3 . C. i . D. 3 .Câu 32. M t ô tô đang ch y v i v n t c 10m/s thì tài x hãm phanh, t th i đi m đó ô tô chuy nộ ạ ớ ậ ố ế ừ ờ ể ểđ ng ch m d n đ u v i v n t c ộ ậ ầ ề ớ ậ ố5 10 m/sv t t , trong đó t là kho ng th i gian tínhả ờb ng giây, k t lúc hãm phanh. H i t lúc hãm phanh đ n khi đ ng h n ô tô còn di chuy nằ ể ừ ỏ ừ ế ừ ẳ ểđ c bao nhiêu mét?ượA. 0,2m B. 2m C. 10m D. 20mCâu 33. S ph c liên h p c a s ph c ố ứ ợ ủ ố ứ4 5 z i làA.4 5 z i . B.4 5 z i . C.4 5 z i . D.4 5 z i .Câu 34. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đ ng th ng ườ ẳ1 2: 2 33 2x td y t tz t . Véc t nàoơd i đây là véc t ch ph ng c a ướ ơ ỉ ươ ủ?dA.1; 2; 3p B. 1; 5;1m C.2; 3; 2n D.2; 3; 3q Câu 35. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể0 ;1; 4A và m t ph ngặ ẳ: 5 2 1 0Q x y z . M t ph ng ặ ẳP qua đi m ểA và song song v i m t ph ng ớ ặ ẳQ cóph ng trình làươ www.thuvienhoclieu .com Trang 4,Oxyz2; 1; 3 ,A4; 0;1B10; 5; 3 .CABC11; 2; 0 .n 2 1; 2; 2 .n 31; 8; 2 .n 41; 2; 2 .n www.thuvienhoclieu .comA. 5 2 6 0x y z . B. 5 2 6 0x y z .C. 5 2 4 0x y z . D. 5 2 6 0x y z .Câu 36. H nguyên hàm c a hàm s ọ ủ ốsiny x x làA. cos sin 2x x x C . B. cos sinx x x C .C. cos sinx x x C . D. cos sinx x x C .Câu 37. Trong không gian v i ớ h t a đ ệ ọ ộOxyz , cho m t ph ng ặ ẳ: 2 4 0P x y z và đ ngườth ng ẳ3: 11x td y tz t t . Tìm kh ng đ nh ẳ ị đúng .A. d và P c t nhau nh ng không vuông góc nhauắ ư .B. d n m trong ằP .C. d và P song song nhau .D. d và P vuông góc nhau .Câu 38. Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đ ng th ng ườ ẳ đi qua đi m ể2; 0; 1M và cóvect ch ph ng ơ ỉ ươ4; 6; 2a . Ph ng trình tham s c a ươ ố ủ làA.2 461 2x ty tz t . B.2 231x ty tz t . C.4 26 32x ty tz t . D.2 231x ty tz t .Câu 39. Trong không gian Oxyz , cho đ ng th ng ườ ẳ1: 2 4 ,3 5x td y t tz t . H i ỏd đi qua đi m nàoểd i đây?ướA. 1; 2; 3 . B. 3; 6; 8 . C. 0; 6; 8 . D. 1; 4; 5 .Câu 40. Cho các hàm s ốf x và g x liên t c trên ụ . Tìm m nh đ ệ ề sai .A. d db aa bf x x f x x . B. d d db b ba a af x g x x f x x g x x .C. d d dc b ba c af x x f x x f x x . D.. d d . db b ba a af x g x x f x x g x x .Câu 41. Hàm s ố( )F x là m t nguyên hàm c a hàm s ộ ủ ố( )f x trên kho ng ả K n uếA. ( ) ( ),F x f x x K . B. ( ) ( ),f x F x x K .C. ( ) ( ),F x f x x K . D. ( ) ( ),f x F x x K . www.thuvienhoclieu .com Trang 5www.thuvienhoclieu .comCâu 42. Ph ng trình m t ph ng ươ ặ ẳP ch a tr c ứ ụOz và c t m t c u ắ ặ ầ S2 2 22 2 2 6 0x y z x y z theo đ ng tròn có bán kính b ng ườ ằ3 làA.0x y . B.0x y . C.2 0x y . D.2 0x y . Câu 43. Cho f x là hàm liên t c trên ụ th a mãn ỏ1 1f và 101d2f t t . Tính20sin 2 . ' sin dI x f x x.A. 12I . B. 1I . C. 12I . D. 1I .Câu 44. Trên m t ph ng t a đặ ẳ ọ ộ Oxy , đ i m bi u di n s ph c liên h p c a s ph cể ể ễ ố ứ ợ ủ ố ứ2 2z i làđi m nào d i đây?ể ướA. 2; 2Q . B.2; 2P . C.2; 2N . D.2; 2M .Câu 45. Ph ng trình ươ22 5 0z z có nghi m ph c ệ ứ1z , 2z . G i ọM , Nl n l t là đi m bi u di nầ ượ ể ể ễc a s ph c ủ ố ứ1z , 2z .Tính MN .A.2MN . B.4MN . C.2MN . D.2 5MN . Câu 46. Tính môđun c a s ph c ủ ố ứ20202z i i .A. 2 2z . B. 5z . C. 10z . D. 10z .Câu 47. Cho hàm s ốy f x liên t c, không âm trên đo n ụ ạ;a b . Th tích ểV c a kh i tròn xoayủ ốđ c t o thành khi quay hình ph ng gi i h n b i đ th c a hàm s ượ ạ ẳ ớ ạ ở ồ ị ủ ốy f x , tr c hoành vàụhai đ ng th ng ườ ẳx a , x b quanh tr c hoành đ c tính theo công th cụ ượ ứA.2baV f x dx . B.2baV f x dx . C.baV f x dx . D.2baV f x dx . Câu 48. G i ọ1 2,z z là nghi m c a ph ng trình ệ ủ ươ22 3 0z z . Giá tr c a bi u th c ị ủ ể ứ2 21 2z z b ngằA . 2 . B. 3 . C. 6 . D. 2 3 .Câu 49. Cho hai s ph c ố ứ11 2 z i và 23 4 z i . Đi m bi u di n c a s ph c ể ể ễ ủ ố ứ1 2 w z z trong m tặph ng t a đ ẳ ọ ộOxy là đi m nào trong các đi m sau?ể ểA.4; 2 .M B.2; 4 .N C.4; 2 .P D.2; 4 .QCâu 50. Xét các s ph c ố ứ z th a mãn ỏ2 4 z i z . Trên m t ph ng t a đặ ẳ ọ ộ Oxy , t p h p các đi mậ ợ ểbi u di n các s ph c ể ễ ố ứ z là đ ng th ng có ph ng trìnhườ ẳ ươA.2 0 x y . B.2 6 0 x y . C.2 0 x y . D.2 3 0 x y www.thuvienhoclieu .com Trang 6www.thuvienhoclieu .com------ H T ------ẾĐÁP ÁN1 2 3 4 5 6 7 8 9 10D B D A C B C C C B11 12 13 14 15 16 17 18 19 20D A A A B D B B C A21 22 23 24 25 26 27 28 29 30C B C B D A B A B C31 32 33 34 35 36 37 38 39 40D C B C B B C D C D41 42 43 44 45 46 47 48 49 50C A D B B D D C A Dwww.thuvienhoclieu.comĐ 2Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: Tính tích phân420tanI xdx .A. 1.3I B. 14I . C. 14I . D. 1ICâu 2: Cho s ph c ố ứ ,z a bi a b tho mãnả1 2 3 2 .i z z i Tính 2 10 .M a bA. 16.M B. 14.M C.13.MD. 1.MCâu 3: Tìm nguyên hàm c a hàm s ủ ố2 3( )2xf xx .A. f x dx 2 7 ln 2x x C B.f x dx2 7 ln 2x C C. f x dx2 7 ln 2x C D. f x dx2 7 ln 2x x C Câu 4: Cho hàm s F(x) là nguyên hàm c a hàm s f(x) trên K. Kh ng đ nh nào sau đây là ố ủ ố ẳ ị sai?A. M i nguyên hàm c a f(x) đ u có d ng F(x) + C.ọ ủ ề ạB. Có duy nh t F(x) là nguyên hàm c a hàm s f(x)ấ ủ ốC. F’(x) = f(x), x K D. F(x) + C cũng là nguyên hàm c a f(x)ủCâu 5: Cho hình v . Di n tích hình ph ng ph n tô đen trên hình v . Hãy ch n đáp án đúnge ệ ẳ ầ e ọA. 60(6 x )S x dx B. 4 60 46 x 6S x dx x x dx C. 4 60 4( ) (6 )S x dx x dx www.thuvienhoclieu .com Trang 7www.thuvienhoclieu .comD. 4 60 4(6 x ) (6 )S x dx x x dx Câu 6: Trong không gian v i h t a đ Oxyzớ ệ ọ ộ , ph ng trình nào sau đây là ph ng trình tham s c aươ ươ ố ủđ ng th ng ∆ đi qua đi m A(1; 4; 7) và vuông góc v i m t ph ng ườ ẳ ể ớ ặ ẳ( ) : 2 2 3 0P x y z A. 12 4 ( )2 7x ty t tz t ¡ B. 1 24 4 ( )7 4x ty t tz t ¡ C. 1 24 4 ( )7 3x ty t tz t ¡ D. 1 24 2 ( )7 3x ty t tz t ¡Câu 7: Tìm tham s ố a đ hàm s ể ố4 3 21 5 5 F x a x ax x là m t nguyên hàm c a hàm sộ ủ ố3 24 6 10 .f x x x xA. 4.a B. 2.a C. 2.a D. 4.aCâu 8: Th tích V c a kh i tròn xoay thu đ c khi quay xung quanh tr c Ox hình ph ng gi i h n b iể ủ ố ượ ụ ẳ ớ ạ ởcác đ ng ườ24 4, 0, 0, 3y x x y x x b ngằA. 35V B. 353V C. 535V D. 335VCâu 9: Cho tích phân 10, 02dxI mx m . Tìm m đ ể 1I .A. 1 18 4m B. 14m C. 104m D. 0mCâu 10: Cho hình thang cong ( )H gi i h n b i cácớ ạ ởđ ng ườ1, 0, 1, 5y y x xx . Đ ng th ngườ ẳx k (1 5k ) chia ( )H thành hai ph n là (ầ1S )và (2S ) ( hình v bênẽ ). Cho hai hình (1S ) và (2S )quay quanh tr c ụOx ta thu đ c hai kh i trònượ ốxoay có th tích l n l t là ể ầ ượ1V và 2V . Xác đ nhịk đ ể1 22V V . A. 15.7k B. 5.3k C. ln 5.k D. 325.kCâu 11: Trong không gian v i h t a đ Oxyz, cho m t c u (S): ớ ệ ọ ộ ặ ầ2 2 22 2 2 0x y z x y z và đi mểA(2; 2; 2). Đi m B thay đ i trể ổ ên m t c u (S). Di n tích c a tam giác OAB có giá tr l n nh t.ặ ầ ệ ủ ị ớ ấA. 1(đvdt) B. 3(đvdt) C. 3(đvdt) D. 2(đvdt)Câu 12: Xét ph ng trình ươ4 23 2 1 0z z trên t p s ph c, kh ng đ nh nào sau đây đúng?ậ ố ứ ẳ ịA. Ph ng trình vô nghi mươ ệ B. Ph ng trình có 3 nghi m ph cươ ệ ứC. Ph ng trình có 2 nghi m th cươ ệ ự D. Ph ng trình có 1 nghi m z = 0ươ ệCâu 13: Trong không gian v i h tr c t a ớ ệ ụ ọ đ ộ Oxyz , cho I(3; -1; 2). Ph ng trình m t c u tâm ươ ặ ầ I, bánkính R = 4 .A. B. C. D. Câu 14: Trong không gian v i h t a đ Oxyz, cho ba đi m ớ ệ ọ ộ ể3; 2;1 , 1; 3; 2 , 2; 4; 3A B C . Tính tíchvô h ng ướ.AB ACuuur uuur. www.thuvienhoclieu .com Trang 8yxO 1k 5S 1S 2f (x)=1/x12345www.thuvienhoclieu .comA. . 2.AB ACuuur uuur B. . 4.AB ACuuur uuur C. . 6AB ACuuur uuur D. . 4.AB ACuuur uuurCâu 15: Trong không gian v i h t a đ Oxyz, xớ ệ ọ ộ ét v trí t ng đ i c a hai đ ng th ngị ươ ố ủ ườ ẳ11 1 12:1 1 3x y zd và 21: 2 2 ( )3x td y t tz t ¡A. 1d và 2d trùng nhau B. 1d và 2d song song C. 1d và 2d c t nhauắ D. 1d và 2d chéo nhauCâu 16: Cho s ph c z = 5 + 2i. Tìm ph n th c và ph n o c a s ph c ố ứ ầ ự ầ ả ủ ố ứzA. Ph n th c b ng 5 và ph n o b ng 2ầ ự ằ ầ ả ằ B. Ph n th c b ng 5 và ph n o b ng -2ầ ự ằ ầ ả ằC. Ph n th c b ng ầ ự ằ - 5 và ph n o b ng -2ầ ả ằ D. Ph n th c b ng 5 và ph n o b ng -2iầ ự ằ ầ ả ằCâu 17: Trong không gian v i h t a đ Oxyz, m t ph ng (P) đi qua g c t a đ và song song v i m tớ ệ ọ ộ ặ ẳ ố ọ ộ ớ ặph ng ẳ: 5 3 2 3 0Q x y z có ph ng trình.ươA. : 5 3 2 0P x y z B. : 5 3 2 0P x y z C. ( ) : 5 3 2 0P x y z D. : 5 3 2 0P x y z Câu 18: Cho bi t ế2f( ) tanx x= liên t c trên t p xác đ nh c a nó và F(x) là m t nguyên hàm c a hàm sụ ậ ị ủ ộ ủ ốf(x). Bi t ế1 34F . Tính ( )3FA. 12 B. 712 C. 112 D. 12Câu 19: Tìm nguyên hàm c a hàm s ủ ố( ) 3 sin 2 cosf x x x .A. f x dx 3cosx - 2sinx + C B. f x dx 3cosx + 2sinx + CC. f x dx -3cosx + 2sinx + C D. f x dx 3cosx + 2sinxCâu 20: Cho s ố ph c ứ1 3z i . S ph c ố ứ1z b ngằA. 1 32 2i B. 1 3i C. 1 3i D. 1 34 4iCâu 21: Trong không gian v i h t a đ Oxyz, cho hai đi m ớ ệ ọ ộ ể2;1; 2M , 4; 5;1N . Tính đ dài đo nộ ạth ng MN.ẳA. MN41 B. MN7 C. MN49 D. MN7Câu 22: Cho s ph c z th a mãn (2 - i)z = (2 + i)(1- 3i). ố ứ ỏ Tìm t a đ đi m M bi u di n choọ ộ ể ể ễ s ph cố ứ ztrong m t ph ng t a đ Oxy.ặ ẳ ọ ộA. ()3; 1M- B. ()3;1M C. ()1; 3M- D. ()1; 3MCâu 23: M t ch t đi m đang chuy n đ ng v i v n t c ộ ấ ể ể ộ ớ ậ ố015 /v m s thì tăng v n t c v i gia t cậ ố ớ ố2 2( ) 4 ( / s )a t t t m . Tính quãng đ ng ch t đi m đó đi đ c trong kho ng th i gian 3s k t lúc b tườ ấ ể ượ ả ờ ể ừ ắđ u tăng v n t c.ầ ậ ốA. 68,25m. B. 69,75m. C. 67,25m. D. 70,25m.Câu 24: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho (2; 1; 0)a , bi t ếb cùng chi u v i ề ớa và có. 10a b . Ch n ph ng án đúngọ ươA. (4; 2; 0)b B. (6; 3; 0)b C. ( 4; 2; 0)b D. ( 6; 3; 0)b www.thuvienhoclieu .com Trang 9www.thuvienhoclieu .comCâu 25: Trong không gian v i h t a đ Oxyzớ ệ ọ ộ , cho đ ng th ng d có ph ng trình tham sườ ẳ ươ ố2: 1 2 ( )5x td y t tz t ¡. Trong các vect sau, vect nào là vect ch ph ng c a đ ng th ng dơ ơ ơ ỉ ươ ủ ườ ẳA. ( 1; 2; 5).u r B. (2;1; 0).vrC. ( 1; 2; 0).b r D. (2;1; 5).a rCâu 26: Hàm nào trong các hàm sau là m t nguyên hàm c a hàm s ộ ủ ố( ) sin 2f x xA. cos2xg x B. cos 2g x x C. cos 22xg x D. cos 22xg xCâu 27: Cho hàm s ố224 5xf xx x . Kh ng đ nh nào sau đây ẳ ị sai?A. 21ln 4 52f x dx x x C B. 21ln 4 52f x dx x x C C. 21ln 4 52f x dx x x C D. 21ln 4 52f x dx x x C Câu 28: Trong không gian v i h t a đ Oxyz, cho đi mớ ệ ọ ộ ể3; 5; 7 , 1;1; 1A B . T a đ trung đi m Iọ ộ ểc a đo n th ng AB.ủ ạ ẳA. 4; 6; 8 .I B. 2; 4; 6 .I C. 1; 2; 3 .I D. 2; 3; 4 .ICâu 29: Cho s ph c ố ứz a bi . Tìm m nh đ đúng trong các m nh đ sauệ ề ệ ềA. 2z z bi B. 2 2.z z a b C. 22z z D. 2z z a Câu 30: Cho hai s ph c ố ứ1 24 2 3 ; .z i z i Tìm ph n o c a s ph c ầ ả ủ ố ứ12 .zzA. 1113. B. 1013. C. 1013. D. 1113.Câu 31: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho vect ơ3 4 2 5AO i j k j . Tìm t a đ c a vectọ ộ ủ ơOAA. 3; 2; 5 B. 3; 17; 2 . C. 3;17; 2 . D. 3; 5; 2 .Câu 32: Tính tích phân 02( )xI x e dx .A. 21e. B. 21e . C. 21e . D. 21e .Câu 33: Bi t r ng t p h p đi m c a s ph c ế ằ ậ ợ ể ủ ố ứ z th a mãn ỏ3 5 z i là m t đ ng tròn ộ ườ.C Tìmt a đ tâm ọ ộI c a ủ.CA. 0 3; .I B. 1 3; .I C. 0 3; .I D. 1 3; .ICâu 34: Cho F(x) là m t nguyên hàm c a hàm s f(x) liên t c trên đo n [a;b]. Kh ng đ nh nào sau đâyộ ủ ố ụ ạ ẳ ịsai ?A. ( ) ( ) ( )baf x dx F b F a B. ( ) 0aaf x dx www.thuvienhoclieu .com Trang 10www.thuvienhoclieu .comC. ( ) ( ) ( )baf x dx F a F b D. ( ) ( )b aa bf x dx f x dx Câu 35: Tìm nguyên hàm c a hàm s ủ ố( ) 2f x x x .A. f x dx22 2 2x x C B. f x dx 22 2 2x x x C C. f x dx22 42 2 2 25 3x x x x C D. f x dx222 2 25x x x C Câu 36: Tính di n tích S c a hình ph ng gi i h n b i đ th c a hai hàm s ệ ủ ẳ ớ ạ ở ồ ị ủ ố3 22 1y x x x và21y x x .A. 1S B. 112S C. 512S D. 5SCâu 37: Trong các s ph c z th a mãn ố ứ ỏ3 4z z i . S ph c có mô đun nh nh t làố ứ ỏ ấA. 3 4 .z i B. 32 .2z i C. 3 4 .z i D. 32 .2z i Câu 38: Trong không gian v i h t a đ Oxyz, ph ng trình m t ph ng qua đi m M(1; 0; 0) và cóớ ệ ọ ộ ươ ặ ẳ ểvect pháp tuy n ơ ế1; 2;1nr có d ng.ạA. 2 2 0x y z B. 2 1 0x y z C. 2 1 0x y z D. 2 0x y z Câu 39: Cho hai s ph c ố ứ14z i và 21 3z i . Tính 1 2z zA. 1 217 10z z B. 1 213z z C. 1 225z z D. 1 25z z Câu 40: Trong không gian Oxyz, cho đ ng th ng ườ ẳ2 1 1: ;2 1 1 2 2x y zmm và m t ph ngặ ẳ( ) : 2 3 0P x y z . Giá tr c a m đ đ ng th ng ∆ song song v i mp(P).ị ủ ể ườ ẳ ớA. 0m B. 1m C. 3m D. 2mCâu 41: Cho s ph c ố ứ22 3z i . Tìm ph n th c và ph n o c a s ph c ầ ự ầ ả ủ ố ứ zA. Ph n th c b ng ầ ự ằ7 và ph n o b ng ầ ả ằ6 2i B. Ph n th c b ng ầ ự ằ7 và ph n o b ng ầ ả ằ6 2C. Ph n th c b ng ầ ự ằ7 và ph n o b ng ầ ả ằ6 2 D. Ph n th c b ng ầ ự ằ7 và ph n o b ng ầ ả ằ6 2iCâu 42: Cho hàm s f(x) liên t c trên [a; d]. Bi t ố ụ ế5; 2d da bf x dx f x dx v i ớa b d thìbaf x dx b ng.ằA. 7 B. 2- C. 3 D. 0Câu 43: Cho tích phân 211(2 1) ln . ( )eI x x dx e ba trong đó *,a b Z . Khi đó a + b b ng:ằA. 1- . B. -3. C. -5. D. 5 . www.thuvienhoclieu .com Trang 11www.thuvienhoclieu .comCâu 44: Trong không gian v i h t a đ Oxyz, cho m t c uớ ệ ọ ộ ặ ầ2 22: 5 4 9S x y z . Tìm t a đọ ộtâm I và bán kính R c a m t c u (S)ủ ặ ầA. 5; 4; 0I và R = 3 B. 5; 4; 0I và R = 3 C. 5; 4; 0I và R = 9 D. 5; 4; 0I và R = 9Câu 45: Gi s tích phân ả ử611ln2 3I dx Mx , tìm M.A. 3M B. 133M C. 3M D. 133MCâu 46: Tính tích phân 202 sinL xdx .A. 2L . B. 1L . C. 1L . D. 2L .Câu 47: Trong không gian v i h t a đ Oxyz, cho m t ph ng ớ ệ ọ ộ ặ ẳ đi qua đi m ể1; 2; 3M và c t ba tiaắOx, Oy, Oz l n l t t i A, B, C sao cho tam giác ầ ượ ạABC đ uề . Ph ng trình m t ph ng ươ ặ ẳ .A. : 2 3 0x y z B. : 2 3 6 0x y z C. : 3 2 6 0x y z D. : 6 0x y z Câu 48: Trong không gian Oxyz, cho hai đi m ể2;1; 2A , 1; 0; 3B . Vi t ph ng trình m t ph ngế ươ ặ ẳP đi qua đi m A sao cho kho ng cách t đi m B đ n m t ph ng ể ả ừ ể ế ặ ẳP l n nh t.ớ ấA. 2 2 9 0x y z B. 3 5 17 0x y z C. 5 3 2 3 0x y z D. 2 5 7 0x y z Câu 49: Trong không gianOxyz , cho hai đi m ể3 3 3 0 2 1; ; , ; ;A B . Tìm t a đ c a đi m ọ ộ ủ ểM thu cộtr c ụOy , bi t ếM cách đ u hai đi m ề ểA và BA. 0 3 0; ; .M B. 3 122 2 ; ; .M C. 110 05 ; ; .M D. 0 1 0, ; .MCâu 50: Cho s ph c ố ứ2 3z i . S ph c liên h p c a ố ứ ợ ủ z có đi m bi u di n ể ể ễ trong m t ph ng Oxy.ặ ẳA. (2; -3) B. (-2; -3) C. (-2; 3) D. (2; 3)---------------------------------------------------------- H T ----------ẾĐÁP ÁN1 B 11 C 21 B 31 B 41 C2 B 12 C 22 A 32 B 42 C3 A 13 C 23 B 33 C 43 D4 B 14 A 24 A 34 A 44 A5 C 15 D 25 A 35 C 45 A6 B 16 B 26 A 36 B 46 A7 C 17 D 27 A 37 D 47 D8 D 18 D 28 D 38 C 48 B9 C 19 C 29 C 39 D 49 C10 A 20 D 30 B 40 D 50 Dwww.thuvienhoclieu.comĐ 3Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờ www.thuvienhoclieu .com Trang 12www.thuvienhoclieu .comCâu 1:F x là m t nguyên hàm c a hàm s ộ ủ ố2.xy xe Hàm s nào sau đây không ph i là ố ảF x ?A. 2122xF x e . B. 2152xF x e .C. 212xF x e C . D. 2122xF x e .Câu 2: Cho đ ng th ng ườ ẳ1 2: 2 ; 3x td y t tz t và đi m ể2; 1; 3I . Đi m ể K đ i x ng v i đi mố ứ ớ ểIqua đ ng th ng ườ ẳ d có t a đọ ộ làA. 4; 3; 3 .K B. 4; 3; 3 .K C. 4; 3; 3 .K D. 4; 3; 3 .KCâu 3: Cho f x , g x là các hàm s xác đ nh và liên t c trên ố ị ụ . Trong các m nh đ sau, m nh đệ ề ệ ềnào sai ?A. d d . df x g x x f x x g x x . B. 2 d 2 df x x f x x .C. d d df x g x x f x x g x x . D. d d df x g x x f x x g x x .Câu 4: Trong không gian v i h tr c ớ ệ ụOxyz , cho đ ng th ng ườ ẳ2 4: 12 3y zd x và m t ph ngặ ẳ: 4 9 9 0P x y z . Giao đi m ểI c a ủd và P làA. 2; 4; 1I . B. 1; 2; 0I . C. 1; 0; 0I . D. 0; 0;1I .Câu 5: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho 2; 3; 1M , 2; 1; 3 N . Tìm t a đ đi m ọ ộ ểEthu c tr c hoành sao cho tam giác ộ ụMNE vuông t i ạ.MA. 2; 0; 0 . B. 0; 6; 0 . C. 6; 0; 0 . D. 4; 0; 0 .Câu 6: Cho hàm s ốf x th a mãn các đi u ki n ỏ ề ệ 2 cos2'f x x và 22f . Tìm kh ng ẳđ nh ị sai trong các kh ng đ nh sauẳ ị ?A. 2 sin2f x x x . B. 0f .C. 02f . D. 12 sin22f x x x .Câu 7: Cho s ph c ố ứz th a mãn ỏ2 0iz i . Kho ng cách t đi m bi u di n c a ả ừ ể ể ễ ủz trên m t ph ngặ ẳt a đ ọ ộOxy đ n đi m ế ể(3; 4)M làA. 2 5 . B. 13 . C. 2 10 . D. 2 2 .Câu 8: Cho hai s ph c ố ứ11 2z i , 24z x yi v i ớ,x y . Tìm c p ặ;x y đ ể2 12z z .A. ; 4; 6x y . B. ; 5; 4x y . C. ; 6; 4x y . D. ; 6; 4x y .Câu 9: Tính di n tích hình ph ng gi i h n b i các đ ng ệ ẳ ớ ạ ở ườ3, 0y x y và hai đ ng th ngườ ẳ1, 2.x x www.thuvienhoclieu .com Trang 13www.thuvienhoclieu .comA. 178 . B. 174 . C. 154 . D. 158 .Câu 10: G i ọ1 2,z z là hai nghi m ph c c a ph ng trình ệ ứ ủ ươ22 2 0z z . Tính 2024 20241 2M z z .A. 0M . B. 10132M . C. 10132M . D. 10122M i .Câu 11: Tính tích phân 120d.1x xIxA. 1ln 2 12I . B. 1 ln 2 I . C. ln 2I . D. 1ln 22I .Câu 12: Trong không gian Oxyz cho các m t ph ng ặ ẳP : x y 2z 1 0, Q : 2x y z 1 0 . G iọ(S) là m t c u có tâm thu c tr c hoành, đ ng th i (S) c t m t ph ng (P) theo giao tuy n làặ ầ ộ ụ ồ ờ ắ ặ ẳ ếm t đ ng tròn có bán kính b ng 2 và (S) c t m t ph ng (Q) theo giao tuy n là m t đ ngộ ườ ằ ắ ặ ẳ ế ộ ườtròn có bán kính b ng r. Xác đ nh r sao cho ch có đúng m t m t c u (S) th a mãn yêu c u.ằ ị ỉ ộ ặ ầ ỏ ầA. 3r .2 B. 5r .2 C. r 3. D. 7r .2Câu 13: Tích phân . Khi đó giá tr ị làA. . B. . C. . D. .Câu 14: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho ba đi m ể1; 1;1 , 2;1; 2 , 0; 0;1A B C . G iọ; ;H x y z là tr ng tâm tam giác ọABC thì giá tr ịx y z là k t qu nào d i đây?ế ả ướA. 1. B. 1. C. 0. D. 2. Câu 15: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho véc t ơ2; 4; 6n . Trong các m t ph ng cóặ ẳph ng trình sau đây, m t ph ng nào nh n véc t ươ ặ ẳ ậ ơn làm véc t pháp tuy n?ơ ếA. 2 6 4 1 0x y z . B. 2 3 0.x y C. 3 6 9 1 0.x y z D. 2 4 6 5 0.x y z Câu 16: Bi t r ng ế ằ102 3ln 22xdx a bx v i ớ,a b Q . Ch n kh ng đ nh ọ ằ ị đúng trong các kh ng đ nhẳ ịsauA. 5a . B. 4b . C. 1a b . D. 2 250a b .Câu 17: Trong không gian v i h tr c to đ ớ ệ ụ ạ ộ cho m t c u ặ ầ có đ ng tròn l n ngo i ti pườ ớ ạ ếtam giác v i ớ Tìm đi m ể n m trên m t c uằ ặ ầ sao cho th tích kh i t di nể ố ứ ệ đ t giá tr l n nh t, bi t ạ ị ớ ấ ế có hoành đ d ng.ộ ươ www.thuvienhoclieu .com Trang 14303sin 2 dI x x xa b a b2012416,OxyzSABC0; 2; 4 ,A4; 1; 1 ,B 4; 5; 1 .C DSABCDDwww.thuvienhoclieu .comA.3; 6; 1 .D B. C. D. Câu 18: Cho 20( ) 5.f x dx Tính 20( ) 2 cos .f x x dxA. 5 . B. 52 . C. 7 . D. 3 .Câu 19: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho ba đi m ể2; 1; 0 , 1; 2; 2A B và 3; 0; 4C .Vi t ph ng trình đ ng trung tuy n đ nh ế ươ ườ ế ỉA c a tam giác ủABC .A. 2 11 2 3x y z . B. 2 11 1 3x y z . C. 2 11 2 3x y z . D. 2 11 2 3x y z .Câu 20: Th tích v t th tròn xoay khi quay hình ph ng gi i h n b i các đ ng ể ậ ể ẳ ớ ạ ở ườtan ,y x0,y0,x3x quanh tr c ụOx b ngằA. 23.3 B. 23 .3 C. 33 . D. 33 . Câu 21: Cho hai m t c u ặ ầ1S , 2S có cùng bán kính R th a mãn tính ch t: Tâm c a ỏ ấ ủ1S thu cộ2S và ng c l i. Tính th tích ph n chung ượ ạ ể ầV c a hai kh i c u t o b i ủ ố ầ ạ ở1( )S và 2( )S .A. 3V R . B. 32RV . C. 3512RV . D. 325RV .Câu 22: M t v t chuy n đ ng v i v n t c ộ ậ ể ộ ớ ậ ốv t , có gia t c là ố23a t t t 2m/s . V n t c ban đ u ậ ố ầc a v t là ủ ậ3m/s . Tính v n t c c a v t sau ậ ố ủ ậ4 giây ?A. 52m/s . B. 75m/s . C. 48m/s . D. 72m/s .Câu 23: Tìm nguyên hàm c a hàm s ủ ố57f x x .A. 65F x x C . B. 635F x x C . C. 435F x x C . D. 676F x x C Câu 24: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đ ng th ng ườ ẳ1: 23 2xd y tz t . Trong các véc t ơ sau,véc t ơ nào có giá song song v i đ ng th ng ớ ườ ẳd ?A. ( 1; 2; 3)u . B. (1; 2; 3)u . C. (0; 2; 4)u . D. (0; 2; 2)u .Câu 25: M t kh i c u có bán kính 5ộ ố ầ dm , ng i ta c t b 2 ph n b ng 2 m t ph ng vuông góc bán ườ ắ ỏ ầ ằ ặ ẳkính và cách tâm 3dm đ làm m t chi c lu đ ng. Tính th tích mà chi c lu ch a đ cể ộ ế ự ể ế ứ ượ .A. 1003( dm 3). B. 132 ( dm 3). C. 41 ( dm 3). D. 43 ( dm 3). www.thuvienhoclieu .com Trang 153; 2; 1 .D 15; 22; 1 .D3; 6; 4 .Dwww.thuvienhoclieu .comCâu 26: Trên m t ph ng ph c, cho đi m ặ ẳ ứ ểA bi u di n s ph c ể ễ ố ứ3 2 ,i đi m ểB bi u di n s ph cể ễ ố ứ1 6 .i G i ọM là trung đi m c a ể ủ.AB Khi đó đi m ểM bi u di n s ph c nào sau đây?ể ễ ố ứA. 1 2 .i B. 2 4 .i C. 2 4 .i D. 1 2 .i Câu 27: Tìm s ph c liên h p c a s ph c ố ứ ợ ủ ố ứ1 4 5 2z i i .A. 13 18z i . B. 13 18z i . C. 13 18z i . D. 13 18z i .Câu 28: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , ph ng trình m t c u ươ ặ ầ S có tâm 1; 2;1I và đi quađi m ể(0; 4; 1)A làA. 2 2 21 2 1 9.x y z B. 2 2 21 2 1 3x y z .C. 2 2 21 2 1 3x y z . D. 2 2 21 2 1 9.x y z Câu 29: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz xét m t c u ặ ầ S đi qua hai đi m ể1; 2;1 , 3; 2; 3 ,A Bcó tâm thu c m t ph ng ộ ặ ẳ: 3 0,P x y đ ng th i có bán kính nh nh t, hãy tính bán kínhồ ờ ỏ ấR c a m t c u ủ ặ ầ.SA. 1.R B. 2.R C. 2.R D. 2 2.RCâu 30: Cho s ph c ố ứ th a mãn ỏ . Tìm mô đun nh nh t c a s ph c ỏ ấ ủ ố ứ .A. . B. . C. . D. .Câu 31: T p h p các đi m trong m t ph ng ph c bi u di n các s ph c ậ ợ ể ặ ẳ ứ ể ễ ố ứ z th a mãnỏ2 2z i z z i làA. Đ ng tròn tâm ườ0;1I , bán kính 1R . B. Đ ng tròn tâm ườ3; 0I , bán kính 3R .C. Parabol 2.4xy D. Parabol 2.4yxCâu 32: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho 2; 3; 0 u , 2; 2; 1 v t a đ c a véc tọ ộ ủ ơ2w u v là www.thuvienhoclieu .com Trang 16z1z z i 2 2w z i 32 23 23 2232www.thuvienhoclieu .comA. 2; 1; 2 . B. 2; 1; 2 . C. 2; 1; 2 . D. 2; 1; 2 .Câu 33: Di n tích hình ph ng gi i h n b i các đ th hàm sệ ẳ ớ ạ ở ồ ị ố3; 2y x x y x và các đ ngườ1; 1x x đ c xác đ nh b i công th cượ ị ở ứA. 1313 d .S x x x B. 1313 d .S x x x C . 0 13 31 03 d 3 d .S x x x x x x D. 0 13 31 03 d 3 d .S x x x x x x Câu 34: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ng ặ ẳ: 2 0P x y . Trong b n m t ố ặph ng sau m t ph ng nào vuông góc v i m t ph ng ẳ ặ ẳ ớ ặ ẳP ?A.1: 2 1 0P x y z . B.3: 2 1 0P x y z .C.2: 1 0P x y z . D.4: 2 0P x y .Câu 35: Cho hàm số( )f x liên t c trênụ và20( ) 2018f x dx . Tính20( ) .I xf x dxA. 2017I . B. 1009I . C. 2018I . D. 1008I .Câu 36: Cho f x là hàm s ch n và ố ẵ03f x dx a . Ch n kh ng đ nh đúng trong các kh ng đ nh sauọ ẳ ị ẳ ịA. 30f x dx a . B. 332f x dx a . C. 33f x dx a . D. 03f x dx a . Câu 37: Hình ph ng gi i h n b i đ th hàm s ẳ ớ ạ ở ồ ị ố22y x x và y x khi quay quanh tr c Ox t oụ ạthành kh i tròn xoay có th tích b ngố ể ằA. 3V . B. 4V . C. V . D. 5V . Câu 38: Trong không gian v i h to đ ớ ệ ạ ộOxyz cho ba đi m ể2; 0; 0A , 0; 3; 0B , 0; 0; 5C . Vi tếph ng trình m t ph ng ươ ặ ẳABC .A. 02 3 5x y z . B. 12 3 5x y z . C. 2 3 5 1x y z . D. 2 3 5 0x y z .Câu 39: Trong không gian Oxyz cho đ ng th ng ườ ẳ1 1 2: .1 2 1x y zd Đ ng th ng ườ ẳd đi quađi m nào d i đây?ể ướA. 1; 2;1M . B. 1; 1; 2N . C. 1;1; 2P . D. 1; 1; 2Q .Câu 40: Cho s ph c ố ứ . Khi đóA. . B. . C. . D. .Câu 41: Tính môđun c a s ph c ủ ố ứ3 4 .z i www.thuvienhoclieu .com Trang 171 3z i 1 1 34 4 iz 1 1 32 2 iz 1 1 32 2 iz 1 1 34 4 iz www.thuvienhoclieu .comA. 5. B. 5. C. 25. D. 1. Câu 42: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho đi m ể1; 1; 3A và hai đ ng th ngườ ẳ1 24 2 1 2 1 1: , : .1 4 2 1 1 1x y z x y zd d Vi t ph ng trình đ ng th ng ế ươ ườ ẳd đi quađi mể,A vuông góc v i đ ng th ng ớ ườ ẳ1d và c t đ ng th ng ắ ườ ẳ2.dA. 1 1 3: .2 1 1x y zd B. 1 1 3: .4 1 4x y zd C. 1 1 3: .2 2 3x y zd D. 1 1 3: .2 1 3x y zd Câu 43: Tính nguyên hàm 1d .2 3xx A. ln 2 3x C . B. 1ln 2 32x C . C. 1ln 2 32x C . D. 2 ln 2 3 .x C Câu 44: Trong không gian v i h tr c t a đ ớ ệ ụ ọ ộOxyz , cho m t ph ng ặ ẳ: 2 2 1 0P x y z và đi mể1; 2; 2M. Tính kho ng cách t đi m ả ừ ểM đ n m t ph ng ế ặ ẳP .A. , 2d M P . B. 2,3d M P C. 10,3d M P D. , 3d M P .Câu 45: Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz , cho hai đi m ể2; 3;1A và 5; 6; 2B . Đ ng th ngườ ẳABc t m t ph ng ắ ặ ẳOxz t i đi m ạ ểM . Tính t s ỉ ốAMBM .A. 13AMBM . B.2AMBM . C. 12AMBM . D.3AMBM .Câu 46: Vi t ph ng trình m t c u có tâm ế ươ ặ ầ1; 2; 3I và ti p xúc v i m t ph ng ế ớ ặ ẳ: 2 2 1 0P x y z . A. 2 2 21 2 3 3x y z . B. 2 2 21 2 3 4x y z .C. 2 2 21 2 3 9x y z . D. 2 2 21 2 3 2x y z .Câu 47: Cho f x , ( )g x là hai hàm s liên t c trên ố ụ . Ch n m nh đ ọ ệ ề sai trong các m nh đ sauệ ềA. ( )d ( )d .b ba af x x f y y B. ( ) ( ) d ( )d ( )d .b b ba a af x g x x f x x g x x C. ( )d 0.aaf x x D. d d d .b c ca a bf x x f x x f x x Câu 48: Tính tích phân 320d21 1x xIx x . www.thuvienhoclieu .com Trang 18www.thuvienhoclieu .comA. 53 . B. 103 . C. 56 . D. 43 .Câu 49: Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz , cho b n đi m ố ể1; 2; 0 , 0; 1;1 , 2;1; 1A B C và3;1; 4D. H i có t t c bao nhiêu m t ph ng cách đ u b n đi m đó?ỏ ấ ả ặ ẳ ề ố ểA. 4 m t ph ng. ặ ẳ B. 6 m t ph ng. ặ ẳ C. 7 m t ph ng. ặ ẳ D. Có 9 m t ph ng.ặ ẳCâu 50: Trong không gian v i h to đ ớ ệ ạ ộOxyz , g i ọ là m t ph ng ặ ẳ đi qua hai đi m ể()2; 0;1A và()2; 0; 5B- đ ng th i h p v i m t ph ng ồ ờ ợ ớ ặ ẳ()Oxz m t góc ộ045 . Kho ng cách t ả ừO t i ớ làA..32 B.3.2 C.1.2 D.2.2----------- H T ----------ẾĐÁP ÁN1 C 11 D 21 C 31 C 41 B2 D 12 A 22 B 32 A 42 A3 A 13 A 23 D 33 C 43 C4 D 14 A 24 C 34 A 44 A5 C 15 D 25 B 35 B 45 C6 A 16 D 26 D 36 B 46 C7 C 17 A 27 D 37 D 47 D8 D 18 C 28 A 38 B 48 B9 B 19 D 29 D 39 B 49 C10 C 20 B 30 C 40 D 50 AH NG D N GI IƯỚ Ẫ ẢCâu 1: Cho hàm số( )f x liên t c trênụ và20( ) 2018f x dx ,tính20( )I xf x dxA. 2017I . B . 1009I . C. 2018I . D. 1008I .L i gi iờ ả2 22 20 0 01 1 1( ) ( ) ( ) 10092 2 2I f x dx f t dt f x dx .Câu 2: Cho hai m t c u ặ ầ1S , 2S có cùng bán kính R th a mãn tính ch t: tâm c a ỏ ấ ủ1S thu cộ2S và ng c l i. Tính th tích ph n chung ượ ạ ể ầV c a hai kh i c u t o b i ủ ố ầ ạ ở1( )S và 2( )S .A. 3V R . B. 32RV . C. 3512RV . D. 325RV .L iờ gi iảG n h tr c ắ ệ ụOxy nh hình vư eKh i c u ố ầ,S O R ch a m t đ ng tròn l n làứ ộ ườ ớ2 2 2:C x y R D a vào hình v , th tích c n tính làự e ể ầ www.thuvienhoclieu .com Trang 19OR2R2 2 2( ) :C x y R yxwww.thuvienhoclieu .com3 32 2 22252 d 23 12 RRRRx RV R x x R x Câu 3: Cho s ph c ố ứ th a mãn ỏ . Tìm mô đun nh nh t c a s ph c ỏ ấ ủ ố ứ .A. . B. . C. . D. .L i gi iờ ảGi s ả ử .Khi đó .Khi đó ..V y mô đun nh nh t c a s ph c ậ ỏ ấ ủ ố ứ là . Câu 4: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz xét m t c u ặ ầ S đi qua hai đi m ể1; 2;1 , 3; 2; 3 ,A Bcó tâm thu c m t ph ng ộ ặ ẳ: 3 0,P x y đ ng th i có bán kính nh nh t, hãy tính bán kínhồ ờ ỏ ấR c a m t c u ủ ặ ầ.SA. 1.R B. 2.R C. 2.R D. 2 2.RG i tâm ọ; 3;I a a b thu c m t ph ng ộ ặ ẳ: 3 0P x y .Do m t c u đi qua hai đi m ặ ầ ể1; 2;1 , 3; 2; 3A B nên IA IB R .Suy ra 2 2 2 2 2 21 5 1 3 5 3 4 4a a b a a b a b b a Khi đó 2 2 2 221 5 3 3 18 35 3 3 8 2 2R a a a a a a .Câu 5: Trong không gian v i h tr c to đ ớ ệ ụ ạ ộ cho m t c u ặ ầ có đ ng tròn l n ngo i ti pườ ớ ạ ếtam giác v i ớ Tìm đi m ể n m trên m t c uằ ặ ầ sao cho th tích kh i t di nể ố ứ ệ đ t giá tr l n nh t, bi t ạ ị ớ ấ ế có hoành đ d ng.ộ ươA.3; 6; 1 .D B. C. D. L i gi iờ ả www.thuvienhoclieu .com Trang 20z1z z i 2 2w z i 32 23 23 2232,z a bi a b z a bi 1z z i 1 1a bi a b i 2 22 21 1a b a b 0a b 2 2w z i 2 2 2 2 2 1a ai i a i a 22 221 9 3 22 2 2 1 8 4 5 2 22 2 2w a a a a a w3 22,OxyzSABC0; 2; 4 ,A4; 1; 1 ,B 4; 5; 1 .C DSABCDD3; 2; 1 .D 15; 22; 1 .D3; 6; 4 .Dwww.thuvienhoclieu .comTa có Nh n th y ậ ấ nên tam giác vuông t i ạDo tam giác n i ti p đ ng tròn l n c a m t c u nên tâm m t c u là trung đi m c aộ ế ườ ớ ủ ặ ầ ặ ầ ể ủ. V y tâm ậ c a m t c u ủ ặ ầ là: bán kính Ph ng trình m t c u ươ ặ ầĐ ể đ t giá tr l n nh t thì ạ ị ớ ấ đ t giá tr l n nh tạ ị ớ ấDo n m trên m t c u nên ằ ặ ầ là giao đi m c a đ ng th ng ể ủ ườ ẳ v i m t c u ớ ặ ầ Trongđó là đ ng th ng qua ườ ẳ và vuông góc v i m t ph ng ớ ặ ẳ+) 1 vect ch ph ng c a ơ ỉ ươ ủ là: ch n là ọ+) Ph ng trình đ ng th ng ươ ườ ẳ và nên: V i ớ (t/m)V i ớ (lo i).ạCâu 6: Trong không gian Oxyz cho các m t ph ng ặ ẳP : x y 2z 1 0, Q : 2x y z 1 0 . G iọ(S) là m t c u có tâm thu c tr c hoành, đ ng th i (S) c t m t ph ng (P) theo giao tuy n làặ ầ ộ ụ ồ ờ ắ ặ ẳ ếm t đ ng tròn có bán kính b ng 2 và (S) c t m t ph ng (Q) theo giao tuy n là m t đ ngộ ườ ằ ắ ặ ẳ ế ộ ườtròn có bán kính b ng r. Xác đ nh r sao cho ch có đúng m t m t c u (S) th a mãn yêu c u.ằ ị ỉ ộ ặ ầ ỏ ầA. 3r .2 B. 5r .2 C. r 3. D. 7r .2L i gi iờ ảG i I là tâm c a (S) và R là bán kính c a (S), ta có: ọ ủ ủ2 2 2 2 2R d I; P 2 d I; Q r N u g i ế ọI x; 0; 0 thì ph ng trình trên đ a t i ươ ư ớ2 22 2x 1 2x 12 r 06 6 C n ch n ầ ọr 0 sao cho ph ng trình b c 2 này có nghi m kép, tìm đ c ươ ậ ệ ượ3r2 www.thuvienhoclieu .com Trang 214; 3; 5 ,AB 4; 3; 5 ,AC 8; 6; 0 .BC . 16 9 25 0AB AC ABC.AABCBCIS0; 2; 1 ,I5.R IA 2 22: 2 1 25.S x y z 1, .S3ABCABCDV d D ABC,d D ABCD Dd.SdI.ABCd, 30; 40; 0AB AC 3; 4; 0 .du3: 2 4 , .1x td y t tz 3 ; 2 4 ; 1D d D t t D S2 29 16 25 1t t t 1 3; 6; 1t D 1 3; 2; 1t D www.thuvienhoclieu .comCâu 7: Trong không gian v i h to đ ớ ệ ạ ộOxyz , g i ọ là m t ph ng ặ ẳ đi qua hai đi m ể()2; 0;1A và()2; 0; 5B- đ ng th i h p v i m t ph ng ồ ờ ợ ớ ặ ẳ()Oxz m t góc ộ045 . Kho ng cách t ả ừO t i ớ làA..32 B.3.2 C.1.2 D.2.2L i gi iờ ảG i ọ;K H l n l t là hình chi u vuông góc đi m ầ ượ ế ể O lên đ ng th ng ườ ẳAB và m t ph ng ặ ẳ().aTa có: ,A B OxzOxz AB OHHK ABOK ABOK AB , ,Oxz KH OK OKH Å45Å0ÅHÅK OSuy ra tam giác OHK vuông cân t i ạHKhi đó: , .2OKd O OH M t khác: ặ3, .2OA ABOK d O ABAB Khi đó: 3, .22OKd O OH www.thuvienhoclieu.comĐ 4Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: M t ch t đi m chuy n đ ng có v n t c tính theo công th c v(t) = 2t + 1 (t là th i gianộ ấ ể ể ộ ậ ố ứ ờtính theo giây). Tính quãng đ ng đi đ c trong kho ng th i gian t giây th 5 đ n giây thườ ượ ả ờ ừ ứ ế ứ10 (quãng đ ng tính theo mét).ườA. 140 m B. 10 m C. 50 m D. 80 mCâu 2: Kho ng ngh ch bi n c a hàm s ả ị ế ủ ố4 212 54y x x là:A. (0; ) B. ( ; 2) và (0; 2) C. ( ; 0) D. ( 2; 0) và (2; )Câu 3: Nguyên hàm c a hàm s : ủ ố2cos .s inxy x là:A. 31sin3x C . B. 31cos3x C C. 3cosx C D. 31cos3x CCâu 4: Trong không gian Oxyz , cho 2 3 4x i j k= + -r r r r . Tìm t a đ c a ọ ộ ủxr:A. (2;3; 4).x= -r B. ( 2; 3;4).x= - -r C. (0; 3; 4).x= -r D. (2;3;0).x=rCâu 5: Nguyên hàm c a ủ( ) 2 1f x x th a mãn ỏ(0) 3F là :A. 2( ) 3F x x x B. 2( ) 3F x x x C. 2( ) 4 3F x x x D. 2( ) 3F x x x www.thuvienhoclieu .com Trang 22www.thuvienhoclieu .comCâu 6: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ngặ ẳ: 2 2 2017 0.P x y z và m t c uặ ầ2 2 2: 2 6 8 10 0;S x y z x y z . Ph ng trình m t ph ng ươ ặ ẳ Q song song v i m t ph ng ớ ặ ẳPvà ti p xúc v i m t c uế ớ ặ ầS là :A. 1: 2 2 25 0Q x y z và 2 : 2 2 1 0.Q x y zB. 1: 2 2 31 0Q x y z và 2: 2 2 5 0.Q x y zC. 1 : 2 2 5 0Q x y z và 2: 2 2 31 0.Q x y zD. 1: 2 2 25 0Q x y z và 2 : 2 2 1 0.Q x y zCâu 7: Xác đ nh các giá tr c a m đê b t ph ng trình ị ị ủ ấ ươ2 2 22 2 29 2 1 6 1 4 0x x x x x xm m nghi m đúng v i m i x th a mãn đi u ki n ệ ớ ọ ỏ ề ệ12x :A. 3m B. 3m C. 3m D. 3mCâu 8: Ch n kh ng đ nh sai trong các kh ng đ nh sau:ọ ẳ ị ẳ ịA. ln10e B. log10 1 C. ln 1e D. ln1 0Câu 9: Tính th tích kh i tròn xoay khi quay quanh Ox mi n D đ c gi i h n b iể ố ề ượ ớ ạ ở32,3xy y x .A. 8135S B. 333035S C. 48635S D. 12152SCâu 10: Cho kh i chóp S.ABCD có SA vuông góc v i đáy, ABCD là hình ch nh t, ố ớ ữ ậAB a ,2AD a , góc gi a SB và m t đáy b ng ữ ặ ằ060 . Th tích c a kh i chóp S.ABC là :ể ủ ốA. 32 33a B. 32 153a C. 22 53a D. 3153aCâu 11: Cho hình chóp t giác S.ABC có th tích b ng V. L y đi m A’ trên c nh SA sao choứ ể ằ ấ ể ạ'SA SA13. M t ph ng qua A’ và song song v i đáy c a hình chóp c t các c nh SB, SC l n l tặ ẳ ớ ủ ắ ạ ầ ượt i B’, C’. Khi đó th tích kh i chóp S.A’B’C’ b ng:ạ ể ố ằA. V27 B. V81 C. V9 D. V3Câu 12: Cho s ph c ố ứ6 7z i . S ph c liên h p c a z có đi m bi u di n là:ố ứ ợ ủ ể ể ễA. 6; 7M B. 6; 7M C. 6; 7M D. 6; 7M Câu 13: Tìm m đ ể3 2( 3) 5y x m x mx m đ t c c ti u t i ạ ự ể ạ2x :A. 2m B. 2m C. 1m D. 0mCâu 14: Trong không gian Oxyz, tìm t a đ hình chi u c a đi m A(-3 ; 2ọ ộ ế ủ ể ; 5) lên m t ph ngặ ẳ( ) : 2 3 5 13 0P x y z :A. H(2; 3 ;4 ) B. H( 3 ; -3 ; 3 ) C. H( -1 ;5 0 ) D. H( 6 ; 4; 1)Câu 15: B t ph ng trình: ấ ươ 2 2log 3x 2 log 6 5x có t p nghi m là:ậ ệ www.thuvienhoclieu .com Trang 23www.thuvienhoclieu .comA. 61;5 B. (1; + ) C. 1;32 D. 3;1Câu 16: Đ i bi n ổ ếs inxu thì tích phân 240sin cosx xdx thành:A. 14 201u u du B. 240u du C. 140u du D. 23 201u u duCâu 17: D i n tích hình ph ng gi i h n b i đ th các hàm sệ ẳ ớ ạ ở ồ ị ố 2; 0; 1; 2y x y x x là :A. 73S B. 53S C. 3S D. 143SCâu 18: Bi t tích phân ế1201.ln 2 . ln 33 2dx a bx x . H i ỏa b b ng :ằA. 1 B. 1 C. 2 D. 5Câu 19: Đi u ki n đ ph ng trình ề ệ ể ươ2 (2 )(2 2) 4 2 2 2x x x m x x cónghi m th c là :ệ ựA. 8; 7m B. 8;17m C. 18; 7m D. 8; 7m Câu 20: Gi s khi đ vào tr ng đ i h c Bách Khoa, m i sinh viên ph i đóng m t kho n banả ử ỗ ườ ạ ọ ỗ ả ộ ảđ u là 10 tri u đ ng. Ông Minh d ki n cho con thi và vào h c t i tr ng này, đ có s ti nầ ệ ồ ự ế ọ ạ ườ ể ố ềđó, gia đình ông đã ti t ki m và hàng tháng g i ngân hàng v i s ti n không đ i, v i lãi su tế ệ ử ớ ố ề ổ ớ ấ0,7%/tháng theo th th c lãi kép. H i đ đ c s ti n trên thì gia đình ph i g i ti t ki m m iể ứ ỏ ể ượ ố ề ả ử ế ệ ỗtháng là bao nhiêu đ sau 12 tháng gia đình đ ti n đóng cho con ăn h c? (làm tròn t i hàngể ủ ề ọ ớngìn)A. 798.000 đB. 833.000 đC. 794.000 đD. 796.000 đCâu 21: Trong không gian Oxyz cho hai đi m M(0;3;7) và I(12;5;0). Tìm t a đ N sao cho I làể ọ ộtrung đi m c a MN :ể ủA. N(0;1;-1). B. N(24;7;-7). C. N(1;2;-5). D. N(2;5;-5).Câu 22: Cho s ph c z = ố ứ1 3i2 2 . S ph c 1 + z + zố ứ 2 b ng:ằA. 1 B. 2 3i C. 1 3i2 2 . D. 0Câu 23: Cho hình chóp tam giác đ u S.ABC có c nh đáy là 2a, c nh bên là 3a. G i V và V’ l nề ạ ạ ọ ầl t là th tích kh i nón đ nh S, đáy là các đ ng tròn n i ti p, ngo i ti p tam giác ABC. Khiượ ể ố ỉ ườ ộ ế ạ ếđó ta có t s ỉ ố'VV b ng :ằA. 1' 2VV B. 4'VV C. 2'VV D. 1' 4VVCâu 24: Hàm s nào d i đây không đ t c c tr ?ố ướ ạ ự ịA. 3 2( ) 3 4f x x x B. 2 3( )1xf xxC. 3 2( ) 3 1f x x x D. 4 2( ) 3f x x x www.thuvienhoclieu .com Trang 24www.thuvienhoclieu .comCâu 25: T p h p các đi m trong m t ph ng bi u di n cho s ph c z tho mãn đi u ki nậ ợ ể ặ ẳ ể ễ ố ứ ả ề ệz 1 2i 4 là:A. M t đ ng th ngộ ườ ẳ B. M t hình vuôngộ C. M t đ ng trònộ ườ D. M t đo n th ngộ ạ ẳCâu 26: Hàm s nào sau đây đ ng bi n trên m i kho ng xác đ nh c a nó:ố ồ ế ỗ ả ị ủA. xy5 B. 3logy x C. xey D. 12logy xCâu 27: Bi t r ng ế ằ1203 2 5x x m dx . H i m b ng bao nhiêu :ỏ ằA. 5 B. 1 C. 1 D. 2Câu 28: S nghi m c a ph ng trình ố ệ ủ ươ5 4 3 23 4 5 20 2017 0x x x x x trên t p h p các sậ ợ ốph c ứ là :A. 0 B. 2 C. 4 D. 5Câu 29: H i ỏtan 2xdx b ng :ằA. 2ln cos 2x C B. 1ln sin 22x C C. 12ln cos 2x C D. 12ln cos 2x CCâu 30: Giá tr nh nh t và giá tr l n nh t c a hàm s ị ỏ ấ ị ớ ấ ủ ố3 2( ) 3 4f x x x trên đo n ạ0; 3 l n l t là:ầ ượA. 0 và 4 . B. 8 và 4 . C. 4 và 4 . D. 8 và 4 .Câu 31: Cho hình chóp S.ABC có tam giác ABC là tam giác đ u c nh b ng 2a. Hình chi u c aề ạ ằ ế ủS trên m t ph ng (ABC) là trung đi m c a c nh AB, góc t o b i c nh SC và m t ph ng đáyặ ẳ ể ủ ạ ạ ở ạ ặ ẳ(ABC) b ng 30ằ 0. Th tích c a kh i chóp S.ABC là:ể ủ ốA. a338 B. a328 C. a334 D. a333Câu 32: Đ tính tích phân ể12011I dxx , hãy ch n cách làm đúng nh t.ọ ấA. Đ t ặtanx t B. Đ t ặsinx t C. Đ t ặ21t x D. Đ t ặ2t xCâu 33: M t hộ ình nón có bán kính đáy 12cm, đ ng cao 16cm. Di n tích xung quanh c a hìnhườ ệ ủnón là :A. 2400cm B. 2160cm C. 2240cm D. 220cmCâu 34: Trong không gian Oxyz cho m t ph ng (P) c t 3 tr c Ox, Oy, Oz l n l t t iặ ẳ ắ ụ ầ ượ ạ2; 0; 0 ; 0; 1; 0 ; 0; 0; 3A B C. Ph ng trình c a m t ph ng (P) là :ươ ủ ặ ẳA. 02 1 3x y z B. 12 1 3x y z C. 12 1 3x y z D. 11 2 3x y z Câu 35: Cho hàm s ố3 2( ) 3 1f x x x . Đ th hàm s c t đ ng th ng ồ ị ố ắ ườ ẳy m t i 3 đi mạ ểphân bi t khi :ệA. 3 1m B. 3 1m C. 3m D. m > 1Câu 36: Trong không gian Oxyz cho M(1;-2;4) và N(-2;3;5). Tính t a đ c a ọ ộ ủMNuuuur:A. MN=uuuur (-3;5;1). B. MN=uuuur (3;-5;-1). C. MN=uuuur (-1;1;9). D. MN=uuuur (1;-1;-9) www.thuvienhoclieu .com Trang 25www.thuvienhoclieu .comCâu 37: Trong không gian Oxyz, cho m t ph ng ặ ẳ (P) có ph ng trình ươ2 2 3 0x y z vàđi m ể1; 3;1M . Ph ng trình m t c u ươ ặ ầ (S) có tâm là M và ti p xúc v i m t ph ng ế ớ ặ ẳ (P) là :A. 2 2 221 3 1 4x y z B. 2 2 21 3 1 4x y z C. 2 2 22 3 1 4x y z D. 2 2 21 3 3 4x y z Câu 38: Trong không gian Oxyz cho M( 2 ; -5 ; 7 ) Tìm t a đ đi m M’đ i x ng c a M quaọ ộ ể ố ứ ủm t ph ng Oxy .ặ ẳA. M’( -22 ; 15 ; -7) B. M’( -4 ; -7 ; -3) C. M’( 2 ; -5 ; -7) D. M’( 1 ; 0; 2)Câu 39: Trong không gian Oxyz cho m t c u (C)ặ ầ có ph ng trình làươ2 2 22 4 6 11 0x y z x y z . Th tích kh i c u (C) là :ể ố ầA. 1253 B. 25003 C. 5009 D. 5003Câu 40: Trong không gian Oxyz cho 3 đi m ể(2; 4; 4), (1;1; 3), ( 2; 0;5)A B C- - - . T a đ đi m D đọ ộ ể ểABCD là hình hình hành là :A. D(1;-3;-4) B. D(-1;-3;-4) C. D(-1;3;4) D. D(1;3;4)Câu 41: Hàm s ố 2x x 2y ln có t p xác đ nh là :ậ ịA. 2;1 B. ; 2 C. ; 2 1; D. 1;Câu 42: Trong không gian Oxyz cho A( – 1; 2; 1), B( – 4; 2; – 2), C( – 1; – 1; – 2). Ph ng trìnhươmp(ABC) là:A. x + y – z = 0 B. x – y + 3z = 0 C. 2x + y + z – 1=0 D. 2x + y – 2z +2= 0Câu 43: G i ọ1z , 2z là 2 nghi m ph c c a ph ng trình ệ ứ ủ ươ0522zz . Tính giá tr c a bi uị ủ ểth c sau ứ2 21 2z z .A. 10 B. 2 10 C. 10 D. 2 5Câu 44: Trong không gian v i h tr c t a đ Oxyz, cho 2 đ ng th ng ớ ệ ụ ọ ộ ườ ẳ11 1 2:2 1 1x y z ,22 1 1:1 2 1x y z . Ph ng trình m t ph ng ch a ươ ặ ẳ ứ1 và song song v i ớ2 là :A. ( ) : 3 6 0P x y z B. ( ) : 3 5 0P x y z C. ( ) : 3 6 0P x y z D. ( ) : 3 16 0P x y z Câu 45: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho m t ph ng ặ ẳ: 2 2 1 0P x y z và đ ngườth ng ẳ1 3: 1 .1x td y tz t Tìm các đi m ểM trên đ ng th ng ườ ẳd sao cho kho ng cách t ả ừM đ n m tế ặph ng ẳP b ng 3.ằA. 1 24; 0; 2 , 2; 2; 0 .M M B. 1 24;1; 2 , 2; 3; 0 .M M C. 1 24; 1; 2 , 2; 3; 0 .M M D. 1 24; 1; 2 , 2; 3; 0 .M M www.thuvienhoclieu .com Trang 26www.thuvienhoclieu .comCâu 46: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho 11: 2 23x td y tz t ; 21 ': 3 2 ' .1x td y tz Xác đ nh vị ịtrí t ng đ i c a hai đ ng th ng ươ ố ủ ườ ẳ1d và 2d .A. Hai đ ng th ng song song.ườ ẳ B. Hai đ ng th ng chéo nhau.ườ ẳC. Hai đ ng th ng c t nhau.ườ ẳ ắ D. Hai đ ng th ng trùng nhauườ ẳCâu 47: Trong không gian Oxyz cho đ ng th ng ườ ẳ15 2: 15x ty tz t và 29 2:2x ty tz t . M t ph ngặ ẳch a c ứ ả1 2, có ph ng trình là :ươA. 3 5 25 0x y z B. 3 5 25 0x y z C. 3 5 25 0x y z D. 3 25 0x y z Câu 48: Tính th tích V c a kh i tròn xoay do hình ph ng gi i h n b i các đ ngể ủ ố ẳ ớ ạ ở ườsin , 0, 0,2xy y x x quay xung quanh tr c Ox là :ụA. 2V B. 22V C. 23V D. 43VCâu 49: Cho ( )F x là m t nguyên hàm c a ộ ủ( ) sin xf x dx và (0) 2F . H i ỏ( )F x b ng :ằA. ( ) cos 2F x x B. ( ) cos 3F x x C. ( ) 2 cos 4F x x D. ( ) cos 1F x x Câu 50: Cho kh i ố lăng tr tam giác đ u ụ ề ABC.A’B’C’ có 2 ; AA ' 3AB a a . Th tích c a kh iể ủ ốlăng tr ABC.A’B’C’ làụA. 3212a B. 33a C. 234a D. 3312a----------- H T ----------ẾĐÁP ÁN1 D 11 A 21 B 31 D 41 C2 D 12 A 22 D 32 A 42 A3 D 13 D 23 D 33 C 43 C4 A 14 C 24 B 34 B 44 C5 A 15 A 25 C 35 A 45 A6 B 16 C 26 B 36 A 46 B7 D 17 C 27 A 37 B 47 C8 A 18 B 28 D 38 C 48 B9 C 19 A 29 D 39 D 49 B10 A 20 D 30 B 40 C 50 Bwww.thuvienhoclieu.comĐ 5Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: Tính mô đun z c a s ph c:ủ ố ứz 4 3i= - www.thuvienhoclieu .com Trang 27www.thuvienhoclieu .comA. z 7.= B. z 5.= C. z 7.= D. z 25.=Câu 2: B n Nam ng i trên máy bay đi du l ch th gi i và v n t c chuy n đ ng c a máy bay làạ ồ ị ế ớ ậ ố ể ộ ủ()()2v t 3t 5 m/s= +. Tính quãng đ ng máy bay đi đ c t giây th 4 đ n giây th 10ườ ượ ừ ứ ế ứA. 1134m. B. 36m. C. 966m. D. 252m.Câu 3: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho hai đi m ể()A 0;1;1 và ()B 1; 2; 3 . Vi t ph ng trìnhế ươm t ph ng ặ ẳ()P đi qua A và vuông góc v i đ ng th ng ớ ườ ẳAB .A. ()P : x 3y 4z 7 0+ + - = . B. ()P : x y 2z 3 0+ + - = .C. ()P : x y 2z 6 0+ + - = . D. ()P : x 3y 4z 26 0+ + - =Câu 4: Cho hàm s ốf (x) th a mãn ỏf (x) 3 5 sin x¢= - và f (0) 10= . M nh đ nào d i đây là ệ ề ướ đúng ?A. f (x ) 3x 5 cos x 2.= + + B. f (x ) 3x 5 cos x 2.= - +C. f (x ) 3x 5 cos x 5.= + + D. f (x) 3x 5 cos x 15.= - +Câu 5: Tìm Mô đun c a s ph c z, bi t: ủ ố ứ ế()21 2i z z 4i 20+ + = -A. 5. B. 7. C. 5. D. 7.Câu 6: Tìm nguyên hàm c a hàm s ủ ố()f x cos 3x=A. sin 3xcos 3xdx C3= - +ò . B. cos 3xdx sin 3x C= +ò .C. sin 3xcos 3xdx C3= +ò . D. cos 3xdx 3 sin 3x C= +ò .Câu 7: Trong không gian v i h t a đ ớ ệ ọ ộOxyz, cho m t ph ng ặ ẳ()P : 3x 4 y 2z 4 0+ + + = và đi mể()A 1; 2; 3-. Tính kho ng cách ảd t đi m ừ ểA đ n m t ph ng ế ặ ẳ()P .A. 5d9=. B. 5d3= . C. 5d29= . D. 5d29= .Câu 8: Trong không gian v i h t a đ Oxyz, cho đ ng th ng ớ ệ ọ ộ ườ ẳx 1 y 2 z 3d :5 8 7- - += =- . Vect nào d iơ ướđây là m t vect ch ph ng c aộ ơ ỉ ươ ủ d ?A. ()a 1; 2; 3 .= - -r B. ()a 7; 8; 5 .= -r C. ()a 1; 2; 3 .= -r D. ()a 5; 8; 7 .= -rCâu 9: Hình ph ng gi i h n b i đ th hai hàm s ẳ ớ ạ ở ồ ị ố2y 2x x= - và y x= khi quay quanh tr c ụOx t oạthành kh i tròn xoay có th tích b ng:ố ể ằA. V .5p= B. V .4p= C. V .3p= D. V .= pCâu 10: Hàm s ố()3xF x e= là m t nguyên hàm c a hàm s :ộ ủ ốA. ()3x2ef x3x= . B. ()3xf x e .= C. ()33 x 1f x x .e-= . D. ()32 xf x 3x .e= .Câu 11: Đ tính tích phân ể2sin x0I e cos xdxp=ò b ng ph ng pháp đ i bi n s , ằ ươ ổ ế ố ta ch n cách đ t nào sauọ ặđây cho phù h p?ợA. Đ t ặt sin x= . B. Đ t ặt cos x= . C. Đ tặ sin xt e= . D. Đ t ặxt e= . www.thuvienhoclieu .com Trang 28www.thuvienhoclieu .comCâu 12: Tính tích phân e1I x ln xdx.=òA. 1I .2= B. 2e 2I .2-= C. 2e 1I .4-= D. 2e 1I .4+=Câu 13: Gi ọ1z là n g hi ệ m ph ứ c c ó ph ầ n ả o âm c ủ a ph ng tươ r ình 2z z 1 0+ + = . T a đ đi m M bi uọ ộ ể ểdi n s ph cễ ố ứ 1z là:A. 1 3M( ; i).2 2- - B. M( 1; 1).- - C. 1 3M( ; ).2 2- -D. 1 3M( ; ).2 2-Câu 14: Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz, giao đi m c a hai đ ng th ng ể ủ ườ ẳx 3 2td : y 2 3tz 6 4tì= - +ïïïï= - +íïï= +ïïî và x 5 t 'd ' : y 1 4t 'z 2 8t 'ì= +ïïïï= - -íïï= -ïïî có t a đ là:ọ ộA. ()3; 7;18 . B. ()3; 2;1 .- C. ()3; 2; 6 .- - D. ()5; 1; 20 .-Câu 15: Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz, cho đ ng th ng ườ ẳx 2 td : y 1 tz tì= -ïïïï= +íïï=ïïî . Ph ng trình nào sauươđây là ph ng trình chính t c c a d ?ươ ắ ủA. x 2 y 1 z.1 1 1- -= =- B. x 2 y z 3.1 1 1+ -= =C. x 2 y z 3.1 1 1+ -= =- D. x 2 y z 3.1 1 1- += =- -Câu 16: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ng ặ ẳ()P : x 2y 2z 24 0- + + = và m t c uặ ầ()()()()2 2 2S : x 1 y 2 z 3 9- + - + - =. V trí t ng đ i c a ị ươ ố ủ()P và ()S là:A. ()P ti p xúc v i ế ớ()S . B. ()P không c t ắ()S .C. ()P đi qua tâm c a ủ()S . D. ()P c t ắ()S .Câu 17: Cho đi m ểI( 3; 0;1)- . M t c u (S) có tâm I và c t m t ph ng ặ ầ ắ ặ ẳ()P : x 2y 2z 1 0+ - - = theo thi t di n làế ệm t đ ng tròn. Di n tích c a hình tròn này b ng ộ ườ ệ ủ ằ p. Vi t ph ng trình m t c u (S).ế ươ ặ ầA. ()()2 22x 3 y z 1 25.+ + + - = B. ()()2 22x 3 y z 1 2.+ + + - =C. ()()2 22x 3 y z 1 4.+ + + - = D. ()()2 22x 3 y z 1 5.+ + + - =Câu 18: N u ế()()f 1 12, f x¢= liên t c ụ trên đo n ạ1; 4 và ()41f ' x dx 17=ò . Giá tr c a ị ủ()f 4 b ng:ằA. 9. B. 5. C. 19. D. 2 9.Câu 19: Trên mp Oxy, t p h p các đi m bi u di n s ph c ậ ợ ể ể ễ ố ứ z tho mãn đi u ki n ả ề ệz 2 3i 5- - = làA. Đ ng tròn ườ()()2 2(C) : x 2 y 3 25.- + - = B. Đ ngườ tròn ()()2 2(C) : x 2 y 3 25.+ + + =C. Đ ng tròn ườ()()2 2(C) : x 2 y 3 25.- + + = D. Đ ng tròn ườ2 2(C) : (x 2) ( y 3) 25.+ + - =Câu 20: Ph ng trình m t c u đ ng kính ươ ặ ầ ườ AB bi t ế A (2; -4; 6), B (4; 2; -2) là? www.thuvienhoclieu .com Trang 29www.thuvienhoclieu .comA. ()()()2 2 2x 3 y 1 z 2 26.- + + + + = B. ()()()2 2 2x 1 y 3 z 2 26.+ + - + - =C. ()()()2 2 2x 3 y 1 z 2 26.+ + + + - = D.()()()2 2 2x 3 y 1 z 2 26.- + + + - =Câu 21: Cho hình ph ng ẳ D gi i h n b i đ ng cong ớ ạ ở ườy 2 cos x= + , tr c hoành và các đ ng th ngụ ườ ẳx 0, x2p= =. Kh i tròn xoay t o thành khi quay ố ạ D quanh tr c hoành có th tích ụ ể V b ng bao nhiêu ?ằA. V ( 1) .= p - p B. V 1.= p + C. V ( 1) .= p + p D. V 1.= p -Câu 22: S ph c ố ứz thay đ i sao cho ổ| z | 1 thì giá tr bé nh t ị ấm và giá tr l n nh t ị ớ ấM c a ủ| z i | làA. m 0, M 2. B. m 1, M 2. C. m 0, M 2. D. m 0, M 1. Câu 23: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể(1; 2; 3)I và m t ph ngặ ẳ()P : 2x 2y z 4 0- - - =. M t c u tâm I ti p xúc v i (P) t i đi m H. Tìm t a đ Hặ ầ ế ớ ạ ể ọ ộ ?A. H( 3; 0; 2).- - B. ()H 1; 4; 4 .- C. ()H 1; 1; 0 .- D. ()H 3; 0; 2 .Câu 24: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai m t ph ng ặ ẳ()P : 2x 3y 4z 20 0- + + = và()Q : 4x 13y 6z 40 0- - + =. V trí t ng đ i c a ị ươ ố ủ()P và ()Q là:A. Trùng nhau. B. C t nh ng không vuông góc.ắ ưC. Vuông góc. D. Song song.Câu 25: Cho A, B, M l n l t là đi m bi u di n c a các s ph c -4; 4i; x-3i ầ ượ ể ể ễ ủ ố ứx R . Tìm giá tr c a xị ủđ A, B, M th ng hàng?ể ẳA. 1.x B. 7.x C. 1.x D. 7.xCâu 26: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , c ho ba đi m ể()A 3; 4; 2- , ()B 5; 6; 2- , ()C 4; 7; 1- - . Tìm t aọđ đi m ộ ểD th a mãn ỏAD 2AB 3AC= +uuur uuur uuur .A. ()D 10;17; 7 .- - B. ()D 10; 17; 7 .- - C. ()D 10; 17; 7 .-D. ()D 10;17; 7 .-Câu 27: Thu g n s ph c ọ ố ứ()2z 2 3i= + đ c:ượA. z 7 6 2i.= - + B. z 11 6 2i.= +C. z 5.= - D. z 1 6 2i.= - +Câu 28: Trong không gian v i h t a đ Oớ ệ ọ ộ xyz , cho hai đi m ểA(1; 2; 3), B( 1; 4;1)- - - và đ ng th ngườ ẳx 2 y 2 z 3d :1 1 2+ - += =-. Ph ng trình nào d i đây là ph ng trình c a đ ng th ng đi qua trungươ ướ ươ ủ ườ ẳđi m đo n th ng ể ạ ẳ AB và song song v i ớ d .A. x y 1 z 11 1 2- += = . B. x y 2 z 21 1 2- += =- .C. x 1 y 1 z 1.1 1 2- - += =- D. x y 1 z 1.1 1 2- += =-Câu 29: Tính tích phân 22 30I x x 1dx= +ò .A. 169 . B. 529 . C. 169- . D. 529- . www.thuvienhoclieu .com Trang 30www.thuvienhoclieu .comCâu 30: Tìm s ph c z th a mãn ố ứ ỏ2(1 i) (2 i) z 8 i (1 2i) z+ - = + + +A. 2 3i.- B. 3 5i.+ C. 1 i.- D. 2 4i.- +Câu 31: Cho s ph c z th a mãn ố ứ ỏ()2 i z 4 3i+ = - Mô đun c a s ph c ủ ố ứw iz 2z= + là:A. 5. B. 41 . C. 5. D. 14.Câu 32: G i ọ1 2,z z là hai nghi m ph c c a ph ng trình ệ ứ ủ ươ2z 2z 13 0- + = . Tính P=2 21 2z z+ ta cók t qu là:ế ảA. 22.P B. 26P . C. 2 13.P D. 0.PCâu 33: Trong không gian Oxyz, m t c u (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có ph ng trìnhặ ầ ươA. 2 2 2(x 1) (y 2) (z 3) 53- + - + + = B. 2 2 2(x 1) (y 2) (z 3) 53+ + + + + =C. 2 2 2(x 1) (y 2) (z 3) 53+ + + + - = D. 2 2 2(x 1) (y 2) (z 3) 53- + - + - =Câu 34: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đ ng th ngườ ẳ : 1x 1 2td : y tz 1 tì= - +ïïïï= -íïï= +ïïî và 2x 1 y 1 z 2d :2 1 1- + -= =- - . V trí t ng đ i c a dị ươ ố ủ1 và d2 là:A. Chéo nhau. B. Trùng nhau. C. C t nhau.ắ D. Song song.Câu 35: Bi t ếa21ln x 1 1I dx ln 2x 2 2= = -ò . Giá tr c a ị ủa b ng:ằA. ln 2 . B. 2 . C. 4 . D. 8 .Câu 36: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai vect ơ()a 1;1; 2= -r , ()b 3; 0; 1= - -r và đi mể()A 0; 2;1. T a đ đi m ọ ộ ểM th a mãn ỏAM 2a b= -uuur r r là:A. ()M 3; 2;1- .B. ()M 5; 4; 2- . C. ()M 5;1; 2- .D. ()M 1; 4; 2- .Câu 37: Tìm t p h p đi m bi u di n s ph c z th a mãn ậ ợ ể ể ễ ố ứ ỏz 2 i z 3i+ + = -A. y x 1.= + B. y x 1.= - + C. y x 1.= - - D. y x 1.= -Câu 38: Tính di n tích hình ph ng gi i h n b i đ th hàm s ệ ẳ ớ ạ ở ồ ị ố3y x x= - và đ th hàm s ồ ị ố2y x x .= -A. 37S .12= B. S 13.= C. 9S .4= D. 81S .12=Câu 39: M t véct pháp tuy n ộ ơ ến c a m t ph ng (Q) ủ ặ ẳx 5y 2 0+ - = có t a đ làọ ộA. ()5;1 2n .;=-rB. ()1; 5 2n .;=-r C. ()1; 0n .5;=r D. ()5; 1n .0;=rCâu 40: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho cho m t ph ng ặ ẳ()P : x 2y 3z 1 0- + - =và đ ng th ngườ ẳx 1 y 2 z 3d :3 3 1- - -= = . Kh ng đ nh nào sau đây ẳ ị đúng ?A. Đ ng th ng d song song v i m t ph ng (P).ườ ẳ ớ ặ ẳ B. Đ ng th ng d n m trong m t ph ng (P).ườ ẳ ằ ặ ẳC. Đ ng th ng d c t m t ph ng (P).ườ ẳ ắ ặ ẳ D. Đ ng th ng d vuông góc v i m t ph ng (P).ườ ẳ ớ ặ ẳCâu 41: Tìm s ph c liên h p ố ứ ợz c a s ph c ủ ố ứz 1 2i.= - +A. z 2 i.= - + B. z 1 2i.= - C. z 1 2i.= - - D. z 1 2i.= + www.thuvienhoclieu .com Trang 31www.thuvienhoclieu .comCâu 42: Tính tích phân: ()251I x 1 x dx= -ò .A. 1I .6= - B. 13I .42= - C. 1I .3= - D. I 0.=Câu 43: Cho s phố ứ c z a bi (a; b )= + Ρ th a mãn:ỏ(3z z)(1 i) 5 z 1 8i.- + - = - + Giá tr ịP a b= - là:A. 1 . B. 6. C. 0. D. 5.Câu 44: Tính tích phân 21ln xI dxx=ò .A. I 2.= B. 2ln 2I .2= C. I ln 2.= D. 2ln 2I .2= -Câu 45: Tính tích phân 21x0I xe dx.=òA. e 1I .2-= B. e 1I .2+= C. eI .2= D. I e.=Câu 46: Tìm s th c ố ự x, y th a: ỏ()()x y 2x y i 3 6i+ + - = -A. x 1; y 4.= = - B. x 1; y 4.= - = - C. y 1; x 4.= - = D. x 1; y 4.= - =Câu 47: Tìm ph n th c a và ph n o b c a s ph c ầ ự ầ ả ủ ố ứ5 4iz 4 3i .3 6i+= - ++A. 73a ,15=17b i .5= - B. 73a ,15=17b .5= C. 17a ,5-=73b .15= D. 73a ,15=17b .5= -Câu 48: Trong không gian v i h t a đ Oớ ệ ọ ộ xyz , cho haiđi m ể(4; 0;1)A và ( 2; 2; 3)B . Ph ng trình nào d i đây là ph ng trình m t ph ng trung tr c c aươ ướ ươ ặ ẳ ự ủđo n th ng ạ ẳAB ?A. 3x y z 6 0.+ + - = B. 3x y z 1 0.- - + =C. 3x y z 0.- - = D. 6x 2y 2z 1 0.- - - =Câu 49: Trong không gian v i h t a đ Oớ ệ ọ ộ xyz , cho đi m ể(3; 1; 2)M và m t ph ngặ ẳ( ) : 3 2 4 0x y z . Ph ng trình nào d i đây là ph ng trình m t ph ng đi qua ươ ướ ươ ặ ẳ M và song songv i ớ( ) ?A. 3x y 2z 14 0.+ - - =B. 3x y 2z 6 0.- - + =C. 3x y 2z 6 0.- + - = D. 3x y 2z 6 0.- + + =Câu 50: Tính tích phân 30I cos x sin xdx.p=òA. 1I .4= - B. 41I .4= - p C. 4I .= - p . D. I 0=---------------------------------------------------------- H T ----------ẾĐÁP ÁN1 B 11 A 21 C 31 B 41 C2 C 12 D 22 A 32 B 42 B3 B 13 C 23 D 33 A 43 D4 C 14 A 24 B 34 B 44 B www.thuvienhoclieu .com Trang 32www.thuvienhoclieu .com5 C 15 A 25 D 35 B 45 A6 C 16 B 26 A 36 B 46 D7 C 17 D 27 A 37 D 47 D8 D 18 D 28 D 38 A 48 C9 A 19 C 29 B 39 C 49 C10 D 20 D 30 A 40 A 50 Dwww.thuvienhoclieu.comĐ 6Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: Tìm th tích ểV c a kh i tròn xoay đ c t o ra khi quay hình thang cong, gi i h n b i đ thủ ố ượ ạ ớ ạ ở ồ ịhàm s ốy f x liên t c trên ụ;a b , tr c ụOx và hai đ ng th ng ườ ẳ x a, x b a b , xung quanh tr cụ.OxA. dbaV f x x.. B. db2aV f x x. C. db2aV f x x. D. dbaV f x x.Câu 2: Trong không gian Oxyz , cho đi m A bi t ể ếOA 2i 3 j k . Khi đó, đi m A có t a đ :ể ọ ộA. A(-2; 3; -1). B. A(-3;2;1). C. A(2;-3;1). D. A(2; -3;2).Câu 3: Cho I=2xxe dx , đ t ặ2u x , khi đó vi t I theo u và du ta đ c:ế ượA. uI 2 e du. B. u1I e du.2 C. uI ue du. D. uI e du.Câu 4: Cho ( )F x là m t nguyên hàm c a hàm s ộ ủ ốxf (x) e 2x th a mãn ỏ3F(0)2 . Tìm F(x) .A. x 23F(x) e x .2 B. x 25F(x) e x .2 C. x 21F(x) e x .2 D. x 21F(x) 2e x .2 Câu 5: Cho s ph c ố ứ4 3z i . Môđun c a s ph c z là:ủ ố ứA. 4. B. 7 . C. 5. D. 3.Câu 6: Trong h t a đ ệ ọ ộ Oxyz , cho đ ng th ng ườ ẳ1 3 1:2 1 1x y zd c t m t ph ngắ ặ ẳ: 2 3 2 0P x y z t i đi m ạ ể; ;I a b c . Khi đó a b c b ngằA. 7. B. 3. C. 5.D. 9 .Câu 7: Tích phân 30I x cos xdx b ng:ằA. 3 1.2 B. 3 1.6 C. 3 1.6 2 D. 3.2 Câu 8: Tính tích 2 s ph c ố ứ1z 1 2i và 2z 3 i A. 3-2i. B. 5 5i . C. 5. D. 5 5i .Câu 9: Cho 2 s ph c ố ứ1 2z 2 i, z 1 i . Tính hi u ệ1 2z zA. 1. B. 2i. C. 1 + 2i. D. 1+iCâu 10: Cho 80f (x )dx 12 . Tính 20I f (4x)dx, .A. I 3. B. I 36. C. I 6. D. I 2. www.thuvienhoclieu .com Trang 33www.thuvienhoclieu .comCâu 11: Trong h t a đ ệ ọ ộ Oxyz , cho đi m ể1;1; 6A và đ ng th ng ườ ẳ2: 1 22x ty tz t . Hình chi u vuôngếgóc c a ủ A trên làA. K 2;1; 0 . B. N 1; 3; 2 . C. H 11; 17;18 . D. M 3; 1; 2 .Câu 12: Trên mp Oxy, t p h p các đi m bi u di n s ph c ậ ợ ể ể ễ ố ứ z tho mãn đi u ki n ả ề ệz 2 3i z 4 i làA. Đ ng th ng: ườ ẳ3x 4y 13 0.. B. Đ ng th ng: ườ ẳ4x 12y 7 0. C. Đ ng th ng: ườ ẳ3x y 1 0. D. Đ ng tròn ườ2 2(C) : (x 2) ( y 3) 25. Câu 13: Trong không gian v i h tr c t a đ ớ ệ ụ ọ ộ Oxyz , cho ba đi m ể( 2; 0; 0), (0; 3; 0)A B và (0; 0; 2)C .Ph ng trình nào d i đây là ph ng trình c a m t ph ng ươ ướ ươ ủ ặ ẳ( )ABC ?A. 1.2 3 2x y z B. 1.2 3 2x y z C. 1.3 2 2x y z D. 1.2 2 3x y z Câu 14: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đ ng th ng ườ ẳ1x 1 2td : y t ..z 1 t và 2x 1 y 1 z 2d :2 1 1 . V trí t ng đ i c a ị ươ ố ủ1d và 2d là:A. Song song. B. C t nhau.ắ C. Chéo nhau. D. Trùng nhau.Câu 15: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho m t c uặ ầ2 22S : x 5 y 4 z 9. Tìm t a đọ ộtâm I và bán kính R c a m t c u ủ ặ ầSA. I 5; 4; 0 và R 9. B. I 5; 4; 0 . và R 3.C. I 5; 4; 0 và R 9. D. I 5; 4; 0 . và R 3.Câu 16: Cho s ph c ố ứz 7 5i . Tìm s ph c ố ứw z iz .A. w 12 2i . B. w 12 12i. . C. w 2 12i . D. w 2 2i .Câu 17: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho ba đi m ểM 1; 2; 3 ; N 3; 2;1 P 1; 4;1 . H i ỏMNPlà tam giác gì?A. Tam giác vuông. B. Tam giác cân. C. Tam giác vuông cân. D. Tam giác đ u.ềCâu 18: Cho 20f x dx 3 .Khi đó 204f x 4 dx b ng:ằA. 6. B. 8. C. 2. D. 4.Câu 19: Cho F x là m t nguyên hàm c a hàm s ộ ủ ố.xf x e Bi t ế0 2,F tính 1 .FA. e. B. 2.e C. 1.e D. 2.Câu 20: Cho s ph c z th a mãn đi u ki n 2z + 3(1 – i)ố ứ ỏ ề ệz = 1 – 9i. Tìm modun c a z.ủA. z 3 . B. z 3 . C. z 13 . D. z 13.Câu 21: Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz , ph ng trình nào d i đây là ph ng trình c a đ ngươ ướ ươ ủ ườth ng đi qua đi m ẳ ểA(2; 3; 0) và vuông góc v i m t ph ng ớ ặ ẳ(P) : x 3y z 5 0 ? www.thuvienhoclieu .com Trang 34www.thuvienhoclieu .comA. 13 ..1x ty tz t B. 1 33 .1 x ty tz t C. 1 33 .1 x ty tz t D. 11 3 ..1x ty tz t Câu 22: Tìm s ph c z bi t r ng ố ứ ế ằ21 1 1.z 1 2i (1 2i) A. 10 35z i.13 26 B. 8 14z i.25 25 C. 10 14z i.13 25 D. 8 14z i.25 25 Câu 23: Cho 2 s ph c ố ứ1 2z 2 i, z 7i . Tính t ng ổ1 2z zA. 2 6i . B. 2 8i . C. 2 6i . D. 2 6i .Câu 24: Ph ng trình m t c u đ ng kính ươ ặ ầ ườ AB bi t A(2; -4; 6), B(4; 2; -2) là?ếA. 2 2 23 1 2 26x y z . B. 2 2 2x 3 y 1 z 2 26. C. 2 2 2x 3 y 1 z 2 26. D. 2 2 2x 3 y 1 z 2 26. Câu 25: Trong không gian v i h t a đ ớ ệ ọ ộOxyz cho m t ph ng ặ ẳ(P) : 2x y 2z 5 0. và t a đ đi mọ ộ ểA(1; 0; 2). Tìm kho ng cách d t đi m ả ừ ể A đ n m t ph ng ế ặ ẳ(P)A. 11d .7 B. 11d .3 C. d 2. D. 11 5d ..5Câu 26: Tìm nguyên hàm c a hàm s ủ ố3 xf x eA. 3 x 3x1e dx e C.3 B. 3 x 3x 11e dx e C.3x 1 C. 3 x 3xe dx 3e C. D. 3 x 3xe dx e C. Câu 27: Cho tích phân e11 3 ln xI dx,x đ t ặt 1 3 ln x . Kh ng đ nh nào sau đây đúng?ẳ ịA. 212I dt.3 B. e12I tdt.3 C. 212I tdt.3 D. 2212I t dt.3Câu 28: M t véct pháp tuy n ộ ơ ến c a m t ph ng (Q):ủ ặ ẳ3 5 2 2019 0.x y z có t a đ làọ ộA. 3; 2; 2 1n .0 9B. 1; 5 2n .; C. 3; 5; 9n .201 D. 3; 5 2n .;Câu 29: Trong không gian v i h t a đ (Oxyz). Cho 2 đi m A(2;2;-3), B(4;0;1).ớ ệ ọ ộ ểKhi đó t a đ trung đi m I c a đo n th ng AB là.ọ ộ ể ủ ạ ẳA. I(1;-1;2). B. I(3;1;-1). C. I(3;-1;-1). D. I(-1;1;2).Câu 30: Tìm các s th c x, y th a mãn: ố ự ỏ(x 2y) (2x 2y)i x y 1 y 3 i . A. x 1, y 1. B. 3 1x , y .4 2 C. 11 1x , y .3 3 D. x 1, y 1. Câu 31: Trong không gian v i h t a đ (Oxyz). Cho A(1; 2; 3), B(2; -1; 1), C(1; 1; -2). Tìm t a đớ ệ ọ ộ ọ ộđi m D sao cho t giác ABCDể ứ là hình bình hành.A. D(2; -2; -4). B. D(2; 0; 6). C. D(0; 4; 0). D. D(2; -2; -4).Câu 32: Di n tích S c a hình ph ng gi i h n b i đ th c a hàm s ệ ủ ẳ ớ ạ ở ồ ị ủ ốy f x liên t c trên ụ;a b , tr cụhoành và hai đ ng th ng ườ ẳx a , x b đ c tính theo công th c:ượ ứ www.thuvienhoclieu .com Trang 35www.thuvienhoclieu .comA. 0 ba 0S f x dx f x dx. B. baS f x dx.C. 0 ba 0S f x dx f x dx. D. baS f x dx.Câu 33: Cho s ph c ố ứ z th a ỏ2 1z . Trong các s ph c ố ứw th a ỏ(3 ) 5w i z i thì s ph c ố ứwcó mô đun l nớ nh t làấA. 6 2 .w i B. 3 2w i . C. 2 6 .w i D. 2 6w i .Câu 34: Tích phân 120I (3x 2x 1)dx b ng:ằA. I 4. B. I 2. C. I 3. D. I 1.Câu 35: Tính I x sin xdx , đ t ặu x , dv sin xdx . Khi đó I bi n đ i thànhế ổA. I x cos x cos xdx. B. I x cos x cos xdx. C. I x sin x cos xdx. D. I x cos x cos xdx. Câu 36: M t v t chuy n đ ng v i v n t c thay đ i theo th i gian đ c tính b i công th cộ ậ ể ộ ớ ậ ố ổ ờ ượ ở ứ v t 3t 2, th i gian tính theo đ n v giây, qu ng đ ng v t đi đ c tính theo đ n v m. Bi t t i th iờ ơ ị ả ườ ậ ượ ơ ị ế ạ ờđi m ểt 2s thì v t đi đ c qu ng đ ng là 10m. H i t i th i đi m ậ ượ ả ườ ỏ ạ ờ ểt 30s thì v t đi đ c qu ngậ ượ ảđ ng là bao nhiêu?ườA. 300m. B. 1410m. C. 1140m. D. 240m.Câu 37: Trong không gian Oxyz, cho 3 vecto a 1;1; 0 ; b 1;1; 0 ; c 1;1;1 . . Trong các m nh đệ ềsau, m nh đ nào sai.ệ ềA. c 3. B. a b. C. b c. D. a 2.Câu 38: Trong h t a đ Oxyz, cho đi m ệ ọ ộ ể3; 5; 3A và hai m t ph ng ặ ẳ: 2 2 8 0P x y z ,: 4 4 0.Q x y z . Vi t ph ng trình đ ng th ng d đi qua A và song song v i c hai m t ph ngế ươ ườ ẳ ớ ả ặ ẳ, .P Q.A. 3: 5 .3 x td yz t B. 3: 5 .3 x td yz t C. 3: 5 .3 x td y tz D. 3: 5 .3 xd y tz tCâu 39: Cho s ph c z th a mãn: ố ứ ỏ4 i z 3 4i . Đi m bi u di n c a ể ể ễ ủz trong m t ph ng t a đ là:ặ ẳ ọ ộA. 16 13M ; i .17 17 B. 16 13M ; .17 17 C. 9 4M ; .5 5 D. 16 11M ; .17 17 Câu 40: Trong không gian Oxyz, m t c u (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có ph ng trìnhặ ầ ươA. 2 2 2(x 1) (y 2) (z 3) 53.. B. 2 2 2(x 1) (y 2) (z 3) 53.. C. 2 2 2(x 1) (y 2) (z 3) 53. D. 2 2 2(x 1) (y 2) (z 3) 53. Câu 41: Gi i ph ng trình :ả ươ24 11 0z z , k t qu nghi m là:ế ả ệ www.thuvienhoclieu .com Trang 36www.thuvienhoclieu .comA. 3 2.3 2.z iz i . B. 1 5.1 5.z iz i . C. 2 7.2 7.z iz i . D. 1 7z i2 21 7z i2 2 .Câu 42: Cho hình ph ng ẳ D gi i h n b i đ ng cong ớ ạ ở ườ2 cosy x , tr c hoành và các đ ng th ngụ ườ ẳ0x, 2x . Tính th tích ểV c a kh i tròn xoay t o thành khi quay ủ ố ạ D quanh tr c hoành.ụA. ( 1)V . B. 1V . C. ( 1)V . D. 1V .Câu 43: Tìm ph n th c và ph n o c a s ph c ầ ự ầ ả ủ ố ứ1z i A. Ph n th c là 1 và ph n o là –i.ầ ự ầ ả B. Ph n th c là 1 và ph n o là 1.ầ ự ầ ảC. Ph n th c là 1 và ph n o là i.ầ ự ầ ả D. Ph n th c là 1 và ph n o là -1.ầ ự ầ ảCâu 44: Trong không gian Oxyz cho đ ng th ng ườ ẳx 1 y 2 z 3d :1 2m 1 2 1(m 0, m )2 và m tặph ng ẳ(P) : x 3y 2z 5 0 . Tìm giá tr ịm đ đ ng th ng ể ườ ẳd vuông góc v i mpớ(P)A. m 2. B. m 1. C. 4m .3 D. m 3.Câu 45: Cho hàm s f(x) có đ o hàm trên đo n [0;3], f(0) = 2 và f(3) = 5 . Tính ố ạ ạ30I f ' x dx .A. 3. B. -9. C. 9. D. -5.Câu 46: Tính di n tích ệS c aủ hình ph ng gi i h n b i đ th hàm s ẳ ớ ạ ở ồ ị ốy x, tr c hoành và đt ụx 4.A. S 8. B. 15S .2 C. S 4. D. S 6.Câu 47: Cho đ ng th ng ườ ẳx y 1 y 3d :2 1 3 và m t ph ng ặ ẳ(P) : x 4 y 2z 6 0. . M nh đ nào d i đây đúng ?ệ ề ướA. d ch a trong (P).ứ B. d và (P) song song. C. d và (P) vuông góc . D. d và (P) c t nhau.ắCâu 48: Trong h t a đệ ọ ộ Oxyz , cho hai đ ng th ng chéo nhau ườ ẳ12 2 6:2 1 2x y zd và 24 2 1:1 2 3x y zd . Ph ng trình m t ph ng ươ ặ ẳP ch a ứ1d và song song v i ớ2d là:A. : 4 3 12 0. P x y z B. : 8 5 16 0. P x y zC. : 2 6 0. P x y D. : 8 5 16 0. P x y zCâu 49: Trong không gian v i h t a đ Oxyz, cho m t ph ng ớ ệ ọ ộ ặ ẳ: 1 0P x y z và đi mểM 1; 2;1 .. M t ph ng (Q) song song v i m t ph ng (P) và kho ng cách t M đ n (P) và (Q) là b ngặ ẳ ớ ặ ẳ ả ừ ế ằnhau thì (Q) có ph ng trình làươA. x y z 5 0. B. x y z 0. C. x y z 7 0.. D. x y z 6 0. Câu 50: Tìm mô đun c a s ph c z th a mãn: ủ ố ứ ỏ(1 3i)z 4i(i 1) 2 5iz A. z 2 3 . B. z 5 . C. z 9 . D. z 2 .----------- H T ----------Ế www.thuvienhoclieu .com Trang 37www.thuvienhoclieu .comĐÁP ÁN1 B 11 D 21 A 31 C 41 C2 C 12 C 22 A 32 B 42 A3 B 13 A 23 D 33 C 43 B4 C 14 A 24 D 34 D 44 B5 C 15 D 25 B 35 B 45 A6 A 16 B 26 A 36 B 46 A7 C 17 D 27 D 37 C 47 B8 D 18 D 28 D 38 A 48 D9 C 19 C 29 B 39 B 49 C10 A 20 D 30 A 40 D 50 Dwww.thuvienhoclieu.comĐ 7Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: Hàm s nào d i đây là h nguyên hàm c a hàm s ố ướ ọ ủ ố1f x x trên 0; .A. 12F x x Cx . B. 3223F x x x C .C. 323F x x x C . D. 12F x Cx .Câu 2: Choy f x , y g x là các hàm s có đ o hàm liên t c trên ố ạ ụ0; 2 và20. d 2g x f x x , 20. d 3g x f x x . Tính tích phân 20. dI f x g x x .A. 5I . B. 1I . C. 1I . D. 6I .Câu 3: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho vect ơ1; 2; 3a . Tìm t a đ c a véctọ ộ ủ ơ2; ;b y z, bi t r ng vect ế ằ ơb cùng ph ng v i vect ươ ớ ơa .A. 2; 4; 6b . B. 2; 4; 6b . C. 2; 4; 6b . D. 2; 3; 3b .Câu 4: Ph ng trình b c hai nào sau đây có nghi m ươ ậ ệ1 2i ?A. 22 5 0z z . B. 22 3 0z z . C. 22 5 0z z . D. 22 3 0z z .Câu 5: Ph ng trình sau có m y nghi m th c: ươ ấ ệ ự22 2 0z z A. 0. B. 2 . C. 3 . D. 1 .Câu 6: Trong không gian t a đ ọ ộOxyz , đ ng th ng đi qua đi m ườ ẳ ể1; 2; 3A và có vect ch ơ ỉph ng ươ2; 1; 2u có ph ng trình làươA. 1 2 32 1 2x y z . B. 1 2 32 1 2x y z . C. 1 2 32 1 2x y z . D. 1 2 32 1 2x y z .Câu 7: Cho s ph c ố ứz a bi ,a b th a mãn ỏ1 311 2ia b ii . Giá tr nào d i đây là ị ướmôđun c a ủz ?A. 5. B. 10 . C. 1 . D. 5 .Câu 8: Trong không gian Oxyz , cho 2 2OA i j k . T a đ đi m ọ ộ ểA là www.thuvienhoclieu .com Trang 38www.thuvienhoclieu .comA. 2; 1; 2A . B. 2; 1; 2A . C. 2; 1; 2A . D. 2; 1; 2A .Câu 9: Tính kho ng cách gi a hai m t ph ng song song ả ữ ặ ẳ( ) : 2 2 4 0x y z và ( ) :2 2 2 0x y z . A. 6 . B. 4.3 C. 2 . D. 10.3Câu 10: Trong không gian Oxyz , m t ph ng đi qua ba đi m ặ ẳ ể2; 0; 0A , 0; 3; 0B , 0; 0; 4C có ph ng trình làươA. 14 3 2x y z . B. 12 3 4x y z . C. 12 3 4x y z . D. 13 2 4x y z .Câu 11: T p h p t t c các đi m bi u di n các s ph c ậ ợ ấ ả ể ể ễ ố ứ zth a mãn: ỏ2 3 2z i là đ ng ườtròn có tâm I và bán kính R l n l t làầ ượA. (2; 3), 2I R . B. (2; 3), 2I R . C. (2; 3), 2I R . D. (2; 3), 2I R .Câu 12: Trong không gian v i h t a đ ớ ệ ọ ộ,Oxyz cho đ ng th ng ườ ẳ1 2 1: .1 2 2x y zd Đi m ểnào d i đây n m trên đ ng th ng ướ ằ ườ ẳ?dA. 1; 2; 5M . B. 1; 0;1N . C. 2; 2; 3E . D. 3; 4; 5F .Câu 13: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , tính kho ng cách t đi m ả ừ ể1; 3; 2M đ n ếđ ng th ng ườ ẳ1 1:1 1 1x y z b ng ằA. 2 . B. 3 . C. 2 2 . D. 2 .Câu 14: Tích phân e11d3I xx b ngằA. ln 4 e 3 . B. ln e 2 . C. ln e 7 . D. 3 eln4 .Câu 15: Cho hai s th c ố ựx , y tho mãn ph ng trình ả ươ2 3 4x i yi . Khi đó giá tr c a ị ủx vày làA. 3x , 2y . B. 3x , 12y i . C. 3x , 12y . D. 3x , 12y .Câu 16: G i ọ1 2,z z là hai nghi m c a ph ng trình ệ ủ ươ22 6 5 0z z trong đó 2z có ph n o âm. ầ ảPh n th c và ph n o c a s ph c ầ ự ầ ả ủ ố ứ1 23z z l n l t làầ ượA. 6;1 . B. 6; 1 . C. 1; 6 . D. 6;1 .Câu 17: Cho 21d 2f x x và 21d 1g x x . Tính 212 3 dI f x g x x b ngằA. 7I . B. 5I . C. 1I . D. 1I . Câu 18: Trong không gian v i h t a đ Oxyz, cho đi m ớ ệ ọ ộ ể4;1; 3A và đ ng th ngườ ẳ1 1 3:2 1 3x y zd . Ph ng trình m t ph ng (P) đi qua A và vuông góc v i đ ng th ng d làươ ặ ẳ ớ ườ ẳA. 2 3 18 0x y z . B. 2 3 16 0x y z . C. 2 3 18 0x y z . D. 2 3 0x y z .Câu 19: Đi m ểM trong hình v bên là đi m bi u di n s ph ce ể ể ễ ố ứA. 1 2z i . B. 2z i .C. 1 2z i . D. 2z i . www.thuvienhoclieu .com Trang 39Oxy21Mwww.thuvienhoclieu .comCâu 20: M t chi c ô tô chuy n đ ng v i v n t c ộ ế ể ộ ớ ậ ố m/sv t , có gia t cố23 m/s1a t v tt . Bi t v n t c c a ô tô t i giây th 5 b ng ế ậ ố ủ ạ ứ ằ6 m/s . Tính v n t c c a ậ ố ủô tô t i giây th 35.ạ ứA. 3ln 6v . B. 6 3ln 6v . C. 3 3 ln 6v . D. 3ln 3 6v .Câu 21: Bi t ế1 2;z z là hai nghi m c a ph ng trình ệ ủ ươ22 3 3 0z z . Khi đó giá tr c a ị ủ2 21 2z z b ngằA. 94 . B. 94 . C. 4 . D. 9 .Câu 22: Cho s ph c ố ứz th a mãn: ỏ23 2 2 4i z i i . Hi u ph n th c và ph n o c a sệ ầ ự ầ ả ủ ốph c ứ z làA. 1 . B. 2 . C. 3 . D. 0 .Câu 23: G i ọ1 2,z z là các nghi m ph c c a ph ng trình ệ ứ ủ ươ23 7 0z z . Khi đó 4 41 2A z z có giá tr b ngị ằA. 13 . B. 23 . C. 13 . D. 23 .Câu 24: Nguyên hàm c a hàm s ủ ố21(2 1)x làA. 31(2 1)Cx . B. 12 4Cx . C. 11 2Cx . D. 12 1Cx .Câu 25: Kh ng đ nh nào sau đây ẳ ị sai ?A. 54d5xx x C . B. 0 dx C . C. e d ex xx C . D. 1d lnx x Cx .Câu 26: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đi m ểA , B v i ớ2; 1; 3OA ,5; 2; 1OB . Tìm t a đ c a vect ọ ộ ủ ơAB .A. 3; 3; 4AB . B. 7;1; 2AB . C. 2; 1; 3AB . D. 3; 3; 4AB .Câu 27: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ng ặ ẳ: 4 4 0P x y z và m t ặc u ầ2 2 2: 4 10 4 0S x y z x z . M t ph ng ặ ẳP c t m t c u ắ ặ ầ S theo giao tuy n là ếđ ng tròn có bán kính b ngườ ằA. 3r . B. 5r . C. 7r . D. 2r .Câu 28: Tính 1201I x x dx đ c k t quượ ế ảA. 23 . B. 2 23 . C. 2 2 13 . D. 23 .Câu 29: Trên t p h p s ph c, ph ng trình ậ ợ ố ứ ươ27 15 0z z có hai nghi m ệ1 2,z z . Giá tr bi u ị ểth c ứ1 2 1 2z z z z làA. –7 . B. 22 . C. 15 . D. 8 . Câu 30: H ọ nguyên hàm c a hàm s ủ ố22 1f x x x làA. 2 2F x x C . B. 3 2123F x x x x C . www.thuvienhoclieu .com Trang 40www.thuvienhoclieu .comC. 3123F x x x C . D. 3 213F x x x x C .Câu 31: Trong các kh ng đ nh sau, kh ng đ nh nào ẳ ị ẳ ị sai ?A. 22 dx x x C . B. cos d sinx x x C . C. e d ex xx C . D. 1d lnx x Cx .Câu 32: Cho hàm s ốy f x có đ o hàm, liên t c trên ạ ụ và 0f x khi0; 5x. Bi tế. 5 1f x f x , tính tích phân 50d1xIf x .A. 52I . B. 53I . C. 10I . D. 54I .Câu 33: N u ế104f x dx thì 102f x dx b ng ằA. 8. B. 2. C. 16. D. 4.Câu 34: Cho 2211 d 2f x x x . Khi đó 52dI f x x b ngằA. 4 . B. 2 . C. 1 . D. 1 .Câu 35: Cho hàm s ốy f x liên t c trên ụ và có đ th nh hình v bên. Hình ph ng đ c ồ ị ư e ẳ ượđánh d u trong hình v bên có di n tích làấ e ệOxycbay f xA. d db ca bf x x f x x . B. d db ba cf x x f x x . C. d db ca bf x x f x x . D. d db ca bf x x f x x .Câu 36: Tính th tích kh i tròn xoay đ c t o thành khi quay hình ph ng gi i h n b i đ th ể ố ượ ạ ẳ ớ ạ ở ồ ịhàm s ố23 y x x và tr c hoành, quanh tr c hoành.ụ ụA. 8510 (đvtt) . B. 87 (đvtt) . C. 8110 (đvtt) . D. 417 (đvtt) .Câu 37: T ng các nghi m ph c c a ổ ệ ứ ủ ph ngươ trình 3 22 0z z làA. 1i . B. 1 . C. 1i . D. 1 .Câu 38: Cho F x là m t nguyên hàm c a hàm s ộ ủ ốf x . Khi đó 1 0F F b ngằA. 10F x dx . B. 10df x x. C. 10 F x dx. D. 10f x dx .Câu 39: Trong không gian v i h tr c ớ ệ ụOxyz , cho 1; 0; 3A , 3; 2;1B . M t ph ng trung tr c ặ ẳ ựđo n ạAB có ph ng trình làươA. 2 1 0x y z . B. 2 1 0x y z . C. 2 1 0x y z . D. 2 1 0x y z . www.thuvienhoclieu .com Trang 41www.thuvienhoclieu .comCâu 40: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , m t ph ng ặ ẳ (P): 9 0ax by cz đi qua hai đi m ể3; 2;1A và 3; 5; 2B , đ ng th i ồ ờ vuông góc v i m t ph ng ớ ặ ẳ: 3 4 0Q x y z . Tính t ng ổ S a b c .A. 12S . B. 2S . C. 4S . D. 2S .Câu 41: Bi tế 5231d ln1 2x x bx ax v i ớa , b là các s nguyên. Tính ố2S a b . A. 10S . B. 5S . C. 2S . D. 2S .Câu 42: Trong không gian Oxyz , cho m t ph ng ặ ẳ: 2 3 1 0P x y z . Vec t nào d i đây là ơ ướm t vec t pháp tu n c a (P) ?ộ ơ ế ủA. 11; 3; 1n . B. 12; 1; 3n . C. 12; 1; 3n . D. 12; 1; 1n .Câu 43: Cho s ph c ố ứ11z i và 22 3z i . Tìm s ph c liên h p c a s ph c ố ứ ợ ủ ố ứ1 2w z z ?A. 3 2w i . B. 1 4w i . C. 1 4w i . D. 3 2w i .Câu 44: Trong không gian Oxyz , cho đ ng th ng ườ ẳ2 1:1 2 1x y zd . Vec t nào d i đây là ơ ướm t vec t ch ph ng c a đ ng th ng d ?ộ ơ ỉ ươ ủ ườ ẳA. 11; 2;1u . B. 22;1; 0u . C. 41; 2; 0u . D. 32;1;1u .Câu 45: Ph ng trình ươ20z az b có m t nghi m ph c là ộ ệ ứ1 2z i . Hi u c a b – a ệ ủ b ngằA. 3 . B. 7 . C. 7. D. 3 .Câu 46: Trong không gian Oxyz, kho ng cách t đi m ả ừ ể1; 2; 2A đ n m t ph ng ế ặ ẳ( ) :2 2 4 0x y z b ngằA. 3. B. 1. C. 1.3 D. 13.3Câu 47: Mô đun c a s ph c ủ ố ứ21 2 2z i i làA. 16 2 . B. 5 2 . C. 4 5 . D. 5 5 .Câu 48: Cho s ph c z th a mãn ố ứ ỏ3 . 7 6i z i z i . Môđun c a s ph c z b ngủ ố ứ ằA. 25 . B. 5. C. 5. D. 2 5 . Câu 49: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t c u ặ ầ S:2 2 26 4 8 4 0x y z x y z . Tìm t a đ tâm ọ ộI và tính bán kính R c a m t c u ủ ặ ầ S.A. 3; 2; 4I ,5R . B. 3; 2; 4I ,25R . C. 3; 2; 4I ,25R . D. 3; 2; 4I ,5R .Câu 50: Cho s ph c ố ứ z th a mãn ỏ3 4z i . Môđun c a ủz b ngằA. 25 . B. 5 . C. 5 . D. 5 5 .------ H T ------ẾĐÁP ÁN1 C 11 C 21 B 31 B 41 D2 A 12 A 22 D 32 A 42 C3 C 13 C 23 D 33 A 43 A4 C 14 D 24 B 34 A 44 A5 A 15 C 25 D 35 A 45 C www.thuvienhoclieu .com Trang 42www.thuvienhoclieu .com6 A 16 B 26 A 36 C 46 B7 A 17 C 27 C 37 B 47 D8 B 18 B 28 C 38 B 48 C9 C 19 D 29 D 39 D 49 A10 B 20 B 30 D 40 C 50 Cwww.thuvienhoclieu.comĐ 8Ề Đ THI TH H C KỲ II Ề Ử ỌMôn: Toán l p 12ớTh i gian: 90 phútờCâu 1: Bi t ế9110f x dx . Giá tr c a ị ủ321.I x f x dx b ngằA. 10. B. 15. C. 5. D. 20.Câu 2: Cho hình ph ng ẳH gi i h n b i đ ng cong ớ ạ ở ườ24y x và tr c ụOx . Tính th tích ểc a kh i tròn xoay t o thành khi cho ủ ố ạH quay quanh tr c ụOx .A. 16.3 B. 32.3 C. 32.5 D. 32.7Câu 3: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , t a đ tâm ọ ộI và bán kính R c a m t c u có ủ ặ ầph ng trình: ươ2 222 3 5x y z là:A. 2; 2; 0 , 5I R B. 2; 3; 0 , 5I R C. 2; 3;1 , 5I R D. 2; 3; 0 , 5I RCâu 4: Cho s ph c z th a mãn ố ứ ỏ1 2 3 5 0i z i . Giá tr bi u th c ị ể ứ.A z z làA. 170.5 B. 170.5 C. 170.5 D. 170.25Câu 5: G i ọ1z , 2z là hai nghi m c a ph ng trình ệ ủ ươ26 10 0z z . Tính 1 2.z zA. 2. B. 4. C. 6. D. 5.Câu 6: Cho s ph c ố ứz a bi th a ỏ2 3z z i . Khi đó a b b ngằA. -1. B. 1. C. -2. D. 0.Câu 7: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho m t ph ng ặ ẳ: 8 0P x y và đi mể( 1; 1; 0)I . M t c u tâm ặ ầI và ti p xúc v i m t ph ng ế ớ ặ ẳ( )P có ph ng trình là:ươA. 2 2 2( 1) ( 1) 50x y z . B. 2 2 2( 1) ( 1) 5 2x y z .C. 2 2 2( 1) ( 1) 50x y z . D. 2 2 2( 1) ( 1) 25x y z .Câu 8: Tích phân 312 1ln 21xdx a bx . Kh ng đ nh nào sau đây đúng?ẳ ịA. 7a b . B. . 12a b . C. 7a b . D. 2ab . www.thuvienhoclieu .com Trang 43www.thuvienhoclieu .comCâu 9: Cho hàm s ốf x có đ o hàm trên đo n ạ ạ0; 3 , 0 2f và 3 5f . Tính30( )I f x dx .A. 9. B. 3. C. 7. D. 10.Câu 10: Tìm c p s th c ặ ố ự( ; )x y th a mãn đi u ki n: ỏ ề ệ( ) (3 ) (3 ) (2 1) ix y x y i x y .A. 4 7;5 5 . B. 4 7;5 5 . C. 4 7;5 5 . D. 4 7;5 5 .Câu 11: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , m t vect ch ph ng c a đ ng th ng ộ ơ ỉ ươ ủ ườ ẳd :21 3x tyz t (t là tham s ) có t a đ là:ố ọ ộA. 1; 2; 3a B. 1; 0; 3a C. 0; 2;1a D. 1; 2;1aCâu 12: Di n tích hình ph ng gi i h n b i đ th các hàm s ệ ẳ ớ ạ ở ồ ị ố22y x x và y x b ngằA. 13.4 B. 7.4 C. 9.4 D. 9.2Câu 13: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đi m ể2; 1; 0 , 4; 3; 6A B . T a đ ọ ộtrung đi m ểI c a đo n ủ ạAB là:A. 1;1; 3I B. 1; 2; 3I C. 3;1; 3I D. 1;1; 3I Câu 14: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đi m ể3; 1;1 , 1; 2; 1A B . M t c u cóặ ầtâm A và đi qua đi m ểB có ph ng trình là:ươA. 2 2 23 1 1 15x y z B. 2 2 23 1 1 17x y z C. 2 2 23 1 1 17x y z D. 2 2 23 1 1 15x y z Câu 15: Tìm nguyên hàm lnxeI dxx .A. ln 2xI e C B. lnxI e C C. lnxI e C D. lnxeI Cx Câu 16: Đ tính ểln 2x x dx th ì ta s d ng ử ụ ph ng phápươA. nguyên hàm t ng ph nừ ầ và đ t ặ2u xdv xdx B. nguyên hàm t ng ph nừ ầ và đ tặln 2u xdv xdx C. đ i bi n s và đ t ổ ế ố ặln( 2)u x D. nguyên hàm t ng ph nừ ầ và đ tặln 2u xdv x dx Câu 17: Tìm công th c ứ sai www.thuvienhoclieu .com Trang 44www.thuvienhoclieu .comA. ( ) ( ) f( ) .b c ca a bf x dx f x dx x dx B. ( ) .b aa bf x dx f x dx C. ( ) ( ) ( ) g( ) .b b ba a af x g x dx f x dx x dx D. ( ) 0aaf x dxCâu 18: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , c ho b a đi m ể2; 3; 1 , 1;1;1 , 1; 1; 3M N P m . V i giá tr nào c a m thì tam giác ớ ị ủ MNP vuông t i ạ N ?A. 3m B. 2m C. 1m D. 0mCâu 19: Đi m ểM trong hình v bên là đi m bi u di n c a s e ể ể ễ ủ ốph c ứ z. Tìm ph n th c và ph n o c a s ph cầ ự ầ ả ủ ố ứ.zA. Ph n th c là 3 và ph n o là −4.ầ ự ầ ảB. Ph n th c là −4 và ph n o là 3ầ ự ầ ả i .C. Ph n th c là −4 và ph n o là 3.ầ ự ầ ảD. Ph n th c là 3 và ph n o là −4ầ ự ầ ả i .Câu 20: Cho hai s ph c ố ứ12 5z i và 21z i , s ph c ố ứ1 2–z z là:A. 3 6 .i B. 1 4 .i C. 1 6 .i D. 3 4 .i Câu 21: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , m t ph ng ặ ẳ( ) : 3 4 0P x y z có m t vectộ ơpháp tuy n là:ếA. (1;1; 3)n B. ( 1; 3; 4)n C. (1; 1; 3)n D. ( 1; 1; 3)n Câu 22: Tìm nguyên hàm c a hàm s ủ ố( ) cos 2f x x x .A. 21( ) sin 22 2xf x dx x C B. 2( ) sin 2 .2xf x dx x C C. 21( ) sin 2 .2 2xf x dx x C D. 2( ) sin 2 .2xf x dx x C Câu 23: Cho ph ng trình ươ20 ( 0, , , )az bz c a a b c R v i ớ24b ac . N u ế0 thì ph ng trình có hai nghi m ph c phân bi t ươ ệ ứ ệ1 2,z z đ c xác đ nh b i công th c nào sau đây?ượ ị ở ứA. 1,22b iza . B. 1,22b iza C. 1,22b iza . D. 1,2b iza .Câu 24: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , ph ng trình chính t c c a đ ng th ng ươ ắ ủ ườ ẳd đi qua đi m ể(1; 2; 5)M và vuông góc v i m t ph ng ớ ặ ẳ( ) : 4 3 2 5 0x y z là:A. 1 2 54 3 2x y z B. 1 2 54 3 2x y z C. 1 2 54 3 2x y z D. 1 2 54 3 2x y z Câu 25: Cho s ph c ố ứ z th a ỏ22 2z i . Trong các k t lu n sau, k t lu n nào đúng.ế ậ ế ậA. .z R B. Mô đun c a ủ zb ng 1.ằC. z có ph n th c và ph n o đ u khác 0.ầ ự ầ ả ề D. zlà s thu n o.ố ầ ảCâu 26: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đ ng th ng ườ ẳ1 3 1:2 1 2x y zd . M t ặph ng ẳQ đi qua đi m ể( 3;1;1)M và vuông góc v i đ ng th ng ớ ườ ẳd có ph ng trình là:ươ www.thuvienhoclieu .com Trang 45www.thuvienhoclieu .comA. 2 2 9 0x y z B. 2 2 9 0x y z C. 2 2 5 0x y z D. 2 2 5 0x y z Câu 27: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể(1; 2; 1)A , đ ng th ngườ ẳ2 2:1 3 2x y zd và m t ph ng ặ ẳ( ) : 2 1 0P x y z . Đ ng th ng đi qua ườ ẳA c t đ ng ắ ườth ng ẳd và song song v i ớ( )P có ph ng trình là:ươA. 1 2 12 9 5x y z B. 1 2 15 2 9x y z C. 1 2 19 2 5x y z D. 1 2 12 9 5x y z Câu 28: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể(0;1; 2)A và hai đ ng th ngườ ẳ1 1: ;2 1 1x y zd và 1: 1 22x td y tz t . Ph ng trình m t ph ng ươ ặ ẳ( )P đi qua A đ ng th i ồ ờsong song v i ớd và d là :A. 2 3 5 13 0x y z . B. 2 6 10 11 0x y z .C. 3 5 13 0x y z . D. 3 5 13 0x y z .Câu 29: G i ọ( )F x là m t nguyên hàm c a hàm s ộ ủ ố28xf xx th a mãn ỏ(2) 0F , khi đó ph ng trình ươ(x)F x có nghi m là:ệA. 1x B. 1x C. 0x D. 1 3x Câu 30: Th tích kh i tròn xoay có đ c do hình ph ng gi i h n b i các đ ng ể ố ượ ẳ ớ ạ ở ườlny x ,0;y 2x quay xung quanh tr c hoành làụA. 2 ln 2 1 B. 2 ln 2 . C. 2 ln 2 1 D. ln 2 1 .Câu 31: Bi t ph ng trình ế ươ20zz ab có m t nghi m là ộ ệ1z i . Môđun c a s ph củ ố ứw a bi là:A. 3 B. 4 . C. 2 2 D. 2 .Câu 32: Cho s ph c ố ứ z th a ỏ4z . Bi t r ng t p h p các đi m bi u di n c a s ph cế ằ ậ ợ ể ể ễ ủ ố ứw 3 4i z i là m t đ ng tròn. Bán kính ộ ườr c a đ ng tròn đó là:ủ ườA. 4.r B. 20.r C. 22.r D. 5.rCâu 33: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho hai đ ng th ng ườ ẳ11 2 3:1 1 1x y zd và23 1 5:1 2 3x y zd . Ph ng trình m t ph ng ch a ươ ặ ẳ ứ1d và 2d làA. 5 4 16 0x y z B. 5 4 16 0x y z C. 5 4 16 0x y z D. 5 4 16 0x y z Câu 34: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , ph ng trình t ng quát c a m t ph ng ươ ổ ủ ặ ẳ( ) qua (2; 1; 4), (3; 2; 1)A B và vuông góc v i ớ: 2 3 0x y z là www.thuvienhoclieu .com Trang 46www.thuvienhoclieu .comA. 11 7 2 21 0x y z . B. 11 7 2 21 0x y z .C. 11 7 2 21 0x y z . D. 11 7 2 21 0x y z .Câu 35: Cho , ,A B C l n l t là ba đi m bi u di n s ph c ầ ượ ể ể ễ ố ứ1 2 3, ,z z z th a ỏ1 2 3.z z z M nhệđ nào sau đây là đúng?ềA. Tam giác ABC là tam giác đ u.ềB. O là tâm đ ng tròn ngo i ti p tam giác ườ ạ ếABC .C. Tr ng tâm tam giácọABC là đi m bi u di n s ph c ể ể ễ ố ứ1 2 3z z z .D. O là tr ng tâm tam giác ọABC .Câu 36: M t thùng r u hình tròn xoay có bán kính trên là 30 ộ ượ ởcm và ởchính gi a là 40 ữcm . Chi u cao thùng r u là 1ề ượm . H i thùng r u đóỏ ượch a đ c t i đa bao nhiêu lít r u (k t qu l y 2 ch s th p phân) ?ứ ượ ố ượ ế ả ấ ữ ố ậCho r ng c nh bên hông c a thùng r u là hình parabol.ằ ạ ủ ượ A. ,321 05 lít. B.,540 01 lít. C. ,201 32 lít. D.,425 16 lít.Câu 37: Cho s ph c ố ứ z th a mãn đi u ki n ỏ ề ệ11iiz . T a đ đi m ọ ộ ểM bi u di n s ph cể ễ ố ứw 2 1z trên m t ph ng làặ ẳA. (2;1)M . B. (1; 2)M . C. (0; 1)M . D. ( 2;1)M .Câu 38: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đi m ể( 2; 0; 2), (0; 3; 3)A B . G i ọ( )P là m t ph ng đi qua ặ ẳA sao cho kho ng cách t đi m ả ừ ểB đ n m t ph ng ế ặ ẳ( )P là l n nh t. Kho ng ớ ấ ảcách t g c t a đ đ n m t ph ng ừ ố ọ ộ ế ặ ẳ( )P b ng:ằA. 214 . B. 314 . C. 414 . D. 514 .Câu 39: Di n tích hình ph ng gi i h n b i đ th ệ ẳ ớ ạ ở ồ ị( )P c a hàm s ủ ố22 3y x x và hai ti p ếtuy n c a ế ủ( )P t i ạ0; 3 , 3; 6A B b ngằA. 72 . B. 92 . C. 174 . D. 94 .Câu 40: Trong không gian v i h t a đ ớ ệ ọ ộOxyz , cho đ ng th ng ườ ẳ1 2:2 1 3x y zd và m t ặph ng ẳ( ) : 2 4 0P x y z . Vi t ph ng trình đ ng th ng ế ươ ườ ẳ n m trong m t ph ng ằ ặ ẳ( )P , đ ng th i c t và vuông góc v i ồ ờ ắ ớd .A. 1 1 15 1 3x y z B. 1 1 15 1 3x y z C. 1 1 15 1 3x y z D. 1 1 15 1 3x y z ----------- H T ----------ẾĐáp án1-C 2-B 3-B 4-D 5-A 6-D 7-C 8-B 9-B 10-D11-B 12-D 13-D 14-C 15-B 16-B 17-A 18-C 19-A 20-A www.thuvienhoclieu .com Trang 47www.thuvienhoclieu .com21-C 22-C 23-B 24-A 25-D 26-A 27-A 28-C 29-D 30-C31-C 32-B 33-D 34-A 35-B 36-D 37-B 38-A 39-D 40-BL I GI I CHI TI TỜ Ả ẾCâu 1 : Đáp án C3 92 21 11 1( ) ( ) ( ) 52 2I f x d x f x dx Câu 2: Đáp án BTh tích kh i tròn xoay là: ể ố22322232(4 ) 43 3xV x dx x Câu 3: Đáp án BCâu 4: Đáp án D7 11 34 170.5 5 5 25z i A z z Câu 5: Đáp án A12236 10 03z iz zz i 1 22 2z z i Câu 6: Đáp án D12 3 3 3 01az z i a bi i a bb Câu 7: Đáp án CBán kính c a m t c u là: ủ ặ ầ10, ( )2d I P Ph ng trình c a m t c u là: ươ ủ ặ ầ2 2 2( 1) ( 1) 50x y z Câu 8: Đáp án B3 3311 12 1 32 2 3 ln 1 4 3 ln 21 1xdx dx x xx x 4, 3 . 12a b a b Câu 9: Đáp án B www.thuvienhoclieu .com Trang 48www.thuvienhoclieu .com30( ) (3) (0) 3I f x dx f f Câu 10: Đáp án D435( ) (3 ) (3 ) (2 1) i3 2 1 75xx y xx y x y i x yx y yy Câu 11: Đáp án BCâu 12 : Đáp án DXét ph ng trình: ươ2023xx x xx Di n tích hình ph ng là: ệ ẳ3 32 20 093 32S x x dx x x dx Câu 13: Đáp án DCâu 14: Đáp án CBán kính m t c u là: ặ ầ17AB V y ph ng trình m t c u là: ậ ươ ặ ầ2 2 23 1 1 17x y z Câu 15: Đáp án Blnln lnxx xeI dx d e e Cx Câu 16: Đáp án BCâu 17: Đáp án ACâu 18: Đáp án C( 3; 2; 2), (2; 2; 2)MN NP m Đ MNP vuông t i N thì ể ạ. 0 6 2 4 4 0 1MN NP m m Câu 19: Đáp án A3 4z i Ph n th c: 3, ph n o: -4ầ ự ầ ảCâu 20: Đáp án A1 26–3z zi Câu 21: Đáp án CCâu 22: Đáp án C www.thuvienhoclieu .com Trang 49www.thuvienhoclieu .com21( ) sin 2 .2 2xf x dx x C Câu 23: Đáp án BCâu 24: Đáp án AĐ ng th ng d vuông góc v i ườ ẳ ớ nên nh n VTPT c a ậ ủ làm VTCP ph ng trình chính t c c a d là: ươ ắ ủ1 2 54 3 2x y z Câu 25: Đáp án D22 2 8z i i Câu 26: Đáp án A(Q) vuông góc v i d nên nh n VTCP c a d làm VTPTớ ậ ủPh ng trình c a (Q): ươ ủ2 2 9 0x y z Câu 27: Đáp án AG i d’ là đ ng th ng c n tìmọ ườ ẳ ầTa có: 232 2x td y tz t G i B là giao đi m c a d’ và d thì ọ ể ủ(2 ; 3 ; 2 2)B t t t (1 ; 3 2; 2 2)AB t t t Đ ng th ng d’ song song v i (P) nên ườ ẳ ớ( )1. 0 2(1 ) 3 2 2 1 03PA n t t t t 2 5; 3;3 3AB 1 VTCP c a d’ là: ủ3 (2; 9; 5)AB V y ph ng trình d’: ậ ươ1 2 12 9 5x y z Câu 28: Đáp án C(P) song song v i d và d’ nên có VTPT là: ớ', (1; 3; 5)d du u Ph ng trình c a (P) là: ươ ủ3 5 13 0x y z Câu 29: Đáp án D2221 (8 )( ) ( ) 828d xF x f x dx x Cx www.thuvienhoclieu .com Trang 50www.thuvienhoclieu .com2(2) 0 2( ) 8 2F CF x x Khi đó: 222( ) 8 2 1 32 4 4 0xF x x x x xx x Câu 30: Đáp án CXét: ln 0 1x x Th tích kh i tròn xoay là: ể ố2 2211 1ln ln 2 ln 2 1V xdx x x dx Câu 31: Đáp án Cph ng trình ươ20zz ab có m t nghi m là ộ ệ11z i nghi m còn l i là: ệ ạ21z i Theo Vi-et: 1 21 22 22a z z ab z z w 2 2 w 2 2i Câu 32: Đáp án BGi s w = a + biả ử2 2w 3 4 w 3 4 w 3 4 . w 20 ( 1) 20i z i i i z i i z i a b V y bán kính c a đ ng tròn là r = 20ậ ủ ườCâu 33: Đáp án DA(1; -2; 3) 1d G i (P) là m t ph ng c n tìmọ ặ ẳ ầVTPT c a (P): ủ1 2, (5; 4;1)d du u Ph ng trình c a (P) là: ươ ủ5 4 16 0x y z Câu 34: Đáp án A(1; 3; 5)AB VTPT c a ủ : , (11; 7; 2)AB n ph ng trình ươ : 11 7 2 21 0x y z Câu 35: Đáp án B www.thuvienhoclieu .com Trang 51www.thuvienhoclieu .comCâu 36: Đáp án DCác đ ng xung quanh thùng r u là các đ ng parabol.ườ ượ ườG i đ ng parabol đó có d ng: ọ ườ ạ2y ax bx c Theo bài ra ta có đ ng parabol này s đi qua các đi m ườ e ể(0; 0, 3), (0, 5; 04), (1; 0, 3) Suy ra: 22 2 35 5 10y x x Th tích thùng r u chính là th tích hình ph ng gi i h n b i đ ng th ng ể ượ ể ẳ ớ ạ ở ườ ẳ22 2 35 5 10y x x ; y = 0; x = 1212 302 2 3 203( ) 425,16( )5 5 10 1500V x x dx m l Câu 37: Đáp án B11 w 2 1 1 2ii z i z iz Câu 38: Đáp án AĐ ể, ( )d B P l n nh t thì ớ ấ( )BA P (2; 3; 1)AB là VTPT c a (P)ủPh ng trình (P) là: ươ2 3 2 0x y z V y ậ2, ( )14d O P Câu 39: Đáp án DCó: ' 2 2y x 2 ph ng trình ti p tuy n t i A và B l n l t là: ươ ế ế ạ ầ ượ2 3, 4 6y x y x 2 ti p tuy n này c t nhau t i Cế ế ắ ạ3; 02 Ph ng trình c a AB: ươ ủ3 0 3x y y x Di n tích c n tìm S b ng di n tích tam giác ABC tr đi di n tích S’ hình ph ng gi i h n b i (P) và ABệ ầ ằ ệ ừ ệ ẳ ớ ạ ởTa có: 274ABCS 3209' 32S x x dx V y ậ27 9 94 2 4S www.thuvienhoclieu .com Trang 52www.thuvienhoclieu .comCâu 40: Đáp án B vuông góc v i d và n m trong (P) nên có VTCP là : ớ ằ( ), (5; 1; 3)P dn u G i ọH d thì ( 1 2 ; ; 2 3 )H t t t , ( l y t a đ theo d )ấ ọ ộMà ( ) 1 2 2 2 3 0 1 (1;1;1)H P t t t t H V y ph ng trình ậ ươ : 1 1 15 1 3x y z www.thuvienhoclieu .com Trang 53
- Xem thêm -